Um den Flächeninhalt und Umfang zusammengesetzter Flächen zu ermitteln, musst Du weder zaubern können noch Albert Einstein sein. Das Ganze ist nämlich gar nicht so schwer, wenn man weiß, wie es funktioniert. Weißt Du nicht? Gar kein Problem, dann schauen wir uns das jetzt einmal ganz genau an! In der Mathe Nachhilfe können wir dem auch nochmal etwas ausführlicher auf den Grund gehen.
Der Umfang zusammengesetzter Flächen
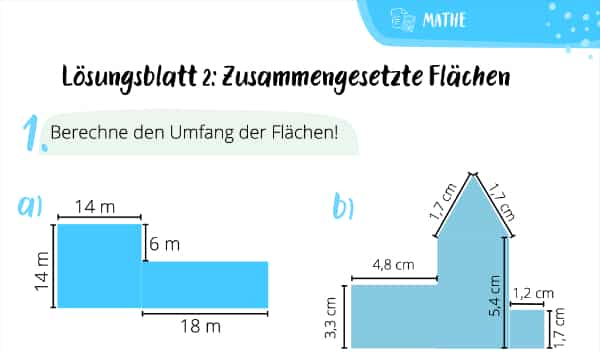
Der Umfang einer Figur ist immer die Länge all seiner Seiten. So auch bei einer zusammengesetzten Fläche. Stell Dir mal vor, Du hast ein Blumenbeet vor Dir. Wenn Du um dieses einmal herumläufst, bist Du seinen Umfang abgegangen. Für Formen wie das Rechteck oder Quadrat gibt es bestimmte Formeln, die wir hierfür benutzen können. Besteht die Fläche hingegen aus mehreren Teilflächen, haben wir keine Formel. Macht aber nichts! Um den Umfang zu bestimmen, addierst Du einfach die einzelnen Seitenlängen.

Der Flächeninhalt zusammengesetzter Flächen
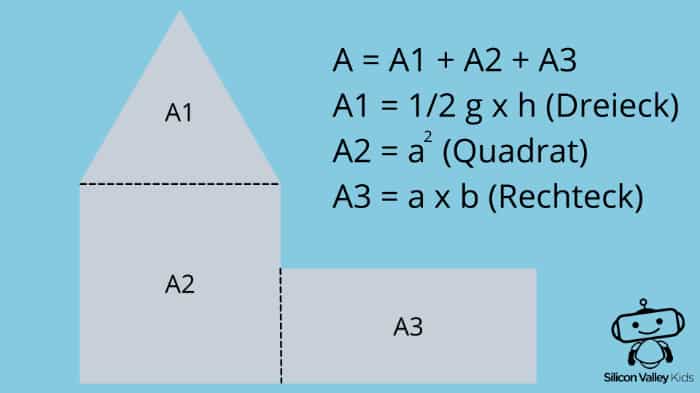
Der Flächeninhalt einer zusammengesetzten Fläche ist immer die Summe seiner Teilflächen. Das bedeutet also: Um den Flächeninhalt zu bestimmen, musst Du erst einmal herausfinden, aus welchen Teilflächen die Figur besteht. Dann ermittelst Du die Größe der Teilflächen, indem Du die entsprechenden Formeln benutzt (etwa für ein Rechteck, Quadrat oder Dreieck). Am Ende addierst Du dann alle Teilflächen und schon hast Du den Flächeninhalt der gesamten Fläche vor der Nase.
Arbeitsblätter & Unterrichtsmaterial
Na, das war doch gar nicht so schwer, oder? Dann lass uns gleich mal schauen, ob Du alles verstanden hast und unsere Übungen lösen kannst. Falls Du noch ein wenig Starthilfe brauchst, leisten wir diese jederzeit in der Nachhilfe für die Grundschule.
Flächeninhalt und Umfang zusammengesetzter Flächen bereiten uns nun kein Kopfzerbrechen mehr! Du weißt schließlich, wie man diese beiden Größen je nach Figur ermitteln kann. Doch falls Du mal nicht weiterweißt, kannst Du jederzeit zu uns zurückkehren und nochmal nachsehen. Bleibt auch unser Geheimnis!
FAQs – Zusammengesetzte Flächen
Eine solche Fläche besteht immer aus mehreren geometrischen Figuren oder Teilfiguren. Sie kann sich dementsprechend etwa aus Quadraten, Rechtecken, Dreiecken, aber auch aus Kreisen, Parallelogrammen und anderen Formen bilden.
Dafür musst Du zuerst herausfinden, aus welchen Teilflächen die gesamte Fläche besteht. Von diesen ermittelst Du dann die einzelnen Flächeninhalte mit den entsprechenden Formeln. Im letzten Schritt werden die Werte der einzelnen Flächeninhalte addiert.
Der Umfang einer jeden geometrischen Figur ist die Summe ihrer Seitenlängen. Du addierst dementsprechend die einzelnen Werte der Seiten und schon hast Du den Umfang ermittelt. Weitere Übungen dazu findest Du auch beim Bildungsserver Hamburg.
Dafür gibt es eine einfache Formel: A = ½ (a + c) × h. Du kannst diese Aufgabe aber auch anders lösen, da ein Trapez aus einem Rechteck und zwei Dreiecken besteht. Ermittelst Du die Flächeninhalte dieser Teilflächen, findest Du also ebenfalls heraus, wie groß die Fläche des Trapezes ist.
Es gibt Flächen unregelmäßiger und regelmäßiger Figuren. Zu den regelmäßigen Figuren gehören etwa Quadrate, Rechtecke, Rauten, Kreise und noch viele mehr.