
Schriftliches Multiplizieren ist gar nicht so schwer, wie Du zunächst befürchtest. In dem folgenden Artikel versorge ich Dich mit einer ausführlichen Schritt-für-Schritt-Anleitung. Die schriftliche Multiplikation basiert darauf, die einzelnen Ziffern einer Zahl zu multiplizieren und die Ergebnisse dann schriftlich zu addieren. Für die Multiplikation der kleinen Zahlen benötigst Du das kleine Einmaleins und es wäre gut, wenn Du schriftliches Addieren bereits beherrschst. All diese Grundlagen zeigen wir Dir auch ausführlich in unserer Mathe Nachhilfe. Lass uns loslegen!
Inhaltsverzeichnis
- Schriftliches Multiplizieren oder mal rechnen
- Schriftlich multiplizieren mit Einern, Zehnern und Hundertern
- Mit Überschlag
- Schriftliche Multiplikation als einfaches Schema
- Multiplikation mehrstelliger Zahlen
- Schriftliche Multiplikation Aufgaben
- Übersicht – Schriftliches Multiplizieren
- Literatur
- FAQs zum Thema schriftlich multiplizieren
Schriftliches Multiplizieren oder mal rechnen
Schriftliches Multiplizieren erfordert gewisse Grundkenntnisse, die Dein Schützling in unserer Hausaufgabenbetreuung vertiefen kann. Bevor wir uns auf dieses spannende Thema stürzen, möchte ich Dich daher gerne zunächst einmal mit den Grundlagen der Multiplikation vertraut machen. Dazu nehmen wir das einfache Beispiel 7 • 4. Wie Du sicher weißt, lautet das Ergebnis 28. In dieser Malaufgabe bezeichnet man die beiden Zahlen 7 und 4 jeweils als Faktor. Das Ergebnis der Malaufgabe nennt man Produkt, in unserem Beispiel also die Zahl 28.
Zusammenfassend kann man also sagen:
7 • 4 = 28
Faktor Faktor Produkt
Schriftlich multiplizieren mit Einern, Zehnern und Hundertern
Für schriftliches Multiplizieren werden wir unsere Faktoren in Einer, Zehner und Hunderter (ggf. auch Tausender und höher, falls die Aufgabe dies verlangt) zerlegen. Die schriftliche Multiplikation basiert dann darauf, die einzelnen Ziffern zu multiplizieren und die Ergebnisse schließlich zu addieren (vgl. Knöß, 1989).

Als Beispiel nehmen wir das Produkt 123 • 3. Dazu zerlegen wir den Faktor 123 zunächst in Hunderter, Zehner und Einer.
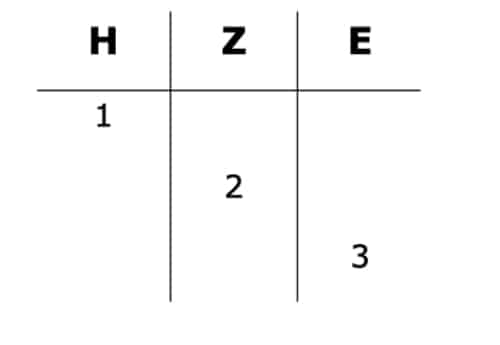
Wie funktioniert das genau? Für die schriftliche Multiplikation multiplizieren wir jede dieser Zahlen mit dem zweiten Faktor, also mit der 3 und erhalten Folgendes:
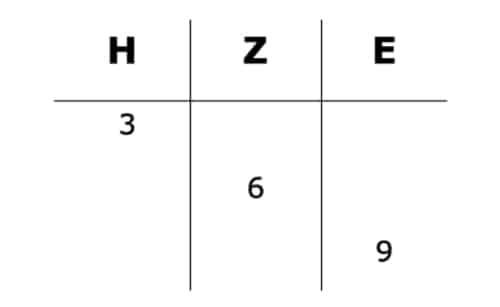
Nun verzeichnet unser Ergebnis 3 Hunderter, 6 Zehner sowie 9 Einer. Demzufolge ergibt unser schriftliches Multiplizieren dann 123 • 3 = 369! Dies ist ein einfaches Beispiel, da unsere Ergebnisse immer eine Stelle haben. Haben Sie mehrere Stellen, so musst Du für die schriftliche Multiplikation nur geeignet verschieben. Dies nennt man Überschlag.
Tatsächlich ist diese Herangehensweise sehr „deutsch“, wie Du z.B. auch der Übersicht der Universität Bremen entnehmen kannst. Dort findest Du auch internationale Varianten zum Thema schriftliche Multiplikation.
Mit Überschlag
Anders als beim obigen Beispiel kann es beim schriftlich multiplizieren vorkommen, dass Deine Zwischenergebnisse mehr als eine Stelle haben. Als Beispiel hierzu möchten wir das Produkt aus 578 • 6 berechnen und zerlegen hierzu wieder in Hunderter, Zehner und Einer.
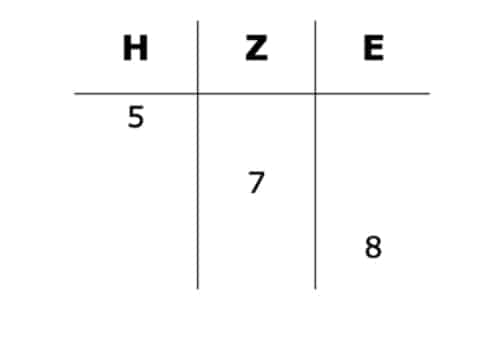
Du willst wissen, wie es weitergeht? Der nächste Schritt ist ganz einfach. Nun musst Du jede Ziffer mit der 6 multiplizieren, da die 6 der 2. Faktor ist.
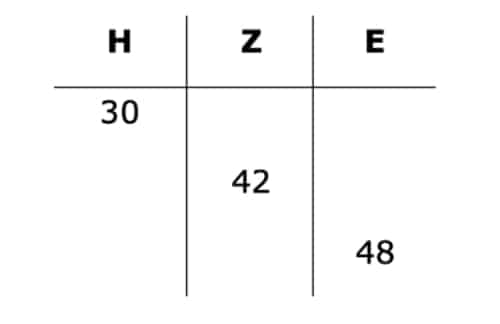
Nun haben wir auch zweitstellige Zwischenergebnisse. Das ist aber kein Problem. Achte darauf, dass Du die Verschiebung korrekt durchführst. Hierzu zeige ich Dir ein Beispiel mit der Zahl 48.

Genauso entsprechen 42 Zehner dann 4 Hundertern und 2 Zehnern. 30 Hunderter bilden 3 Tausender und 0 Hunderter. Du kannst also einfach jede Stelle „zu viel“ um eine nach links verschieben.
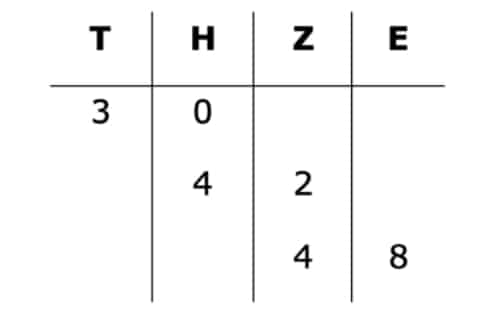
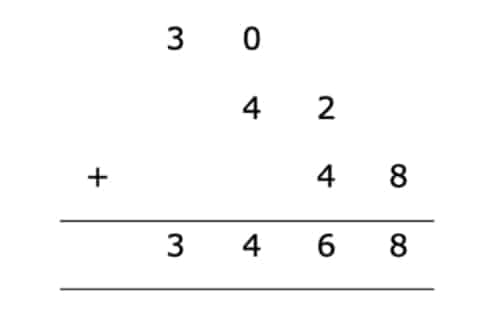
Nun hast du es fast geschafft. Es fehlt nur noch ein Schritt bis zum Ergebnis. Anschließend musst Du die Zahlen addieren um das die Lösung zu erhalten.
Schriftliche Multiplikation als einfaches Schema
Nun beherrschst Du die Grundlagen für schriftliches Multiplizieren. Ich zeige Dir nun, dass Du die schriftliche Multiplikation auch etwas schneller als einfaches Schema umsetzen kannst. Anschließend vertiefen wir dies mithilfe von Beispielen. Anstelle der Verschiebung, kannst Du Deine Zwischenergebnisse auch „an die richtige Stelle“ bringen, indem Du Nullen ergänzt (vgl. Padberg/Büchter, 2015). Dazu verwenden wir die gleich Methode wie oben, ergänzen jedoch Nullen an den leeren Stellen. Wir nehmen wieder das Beispiel 578 • 6:
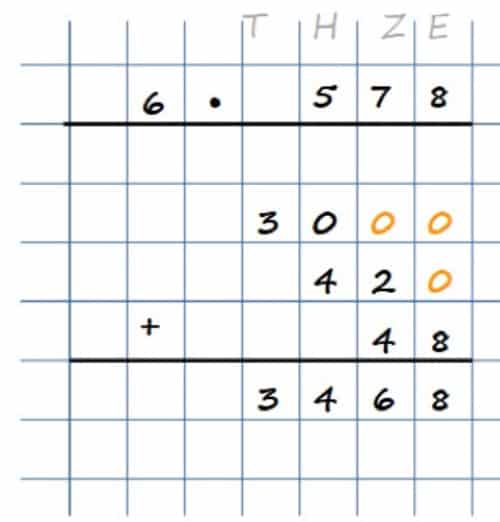
Dass das erste Ergebnis gleich 30 ist, siehst Du bestimmt ganz schnell. Da die Ziffer 5 in dem zweiten Faktor als Hunderter vorkommt, musst Du zwei Nullen ergänzen (da es ja Hunderter sind). Danach berechnen wir 6 • 7 = 42. Da die 7 in dem zweiten Faktor als Zehner vorkommt, ergänzt Du also eine 0. Die 420 schreiben wir dann gemäß unserer Tabelle unter die 3000. Als letztes multiplizieren wir die 6 mit der 8 und erhalten 48, was wir dann wieder passend eintragen. Das Addieren der drei Produkte ergibt dann unser Ergebnis 3468!
Schritte in Kurzfassung
Bevor wir weitermachen, möchte ich Dir noch die folgenden vier Schritte an die Hand geben, damit deine Schriftliche Multiplikation aufgeht!
1. Multipliziere den 1. Faktor mit der ersten Ziffer des 2. Faktors
2. Ergänze Nullen, je nachdem ob Du mit den Hundertern, Zehnern oder Einern multipliziert hast.
3. Sobald Du bei den Einern angelangt bist, bist Du mit der Multiplikation fertig
4. Dein Ergebnis erhältst Du, indem Du Deine Zwischenergebnisse addierst
Lass uns schriftliches Multiplizieren nun anhand eines weiteren Beispiels üben! Diesmal nehmen wir 9 • 458:
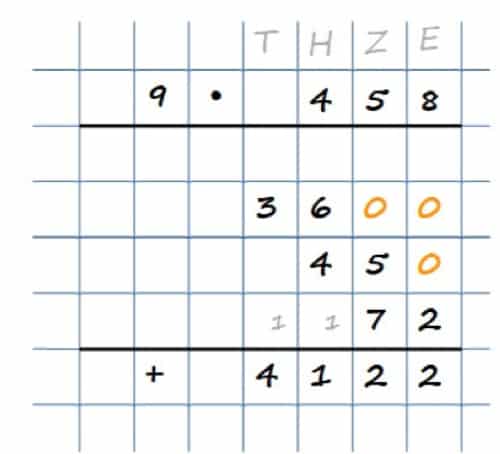
Hier kannst Du genauso vorgehen wie im vorherigen Beispiel. Du wirst Deine schriftliche Multiplikation stets richtig ausführen, solange Du Dich an die folgenden vier Schritte hältst:
- Multipliziere die 9 (erster Faktor) mit der ersten Ziffer des 2. Faktors, also mit der 4. Dies ergibt 36.
- Da die 4 als Hunderter vorkommt, ergänzen wir zwei Nullen
- Wiederhole dies mit den nächsten Ziffern. Wenn Du ebenfalls als erstes Ergebnis 45 erhältst, dann hast Du richtig gerechnet. Falls Du dieses Ergebnis auch hast, ergänze eine Null. Danach solltest du 72 erhalten, bei welcher Du keine 0 zu ergänzen brauchst.
- Nachdem Du all die oben genannten Schritte erfolgreich gemeistert hast, musst Du noch die Zwischenergebnisse addieren und Du erhältst Dein Endergebnis 4122!
Multiplikation mehrstelliger Zahlen
Das Schema schriftliche Multiplikation eignet sich prima auch dann, wenn der erste Faktor mehrstellig ist. Wir müssen beim schriftlich Multiplizieren dann nur korrekt verschieben und entsprechend anpassen. Wie das geht, zeige ich Dir jetzt am Beispiel 23 • 314!
Nachdem wir wieder wie im ersten Schritt die 3 mit der 314 multipliziert haben, schreiben wir die Ergebnisse darunter. Im zweiten Schritt multiplizieren wir die 2 mit der 314, aber verschieben die Ergebnisse um 1 nach links, da auch die 2 (erster Faktor) eine Stelle weiter links steht: nämlich an der Zehnerstelle. Wie oben addieren wir dann alles, um das Ergebnis zu erhalten.
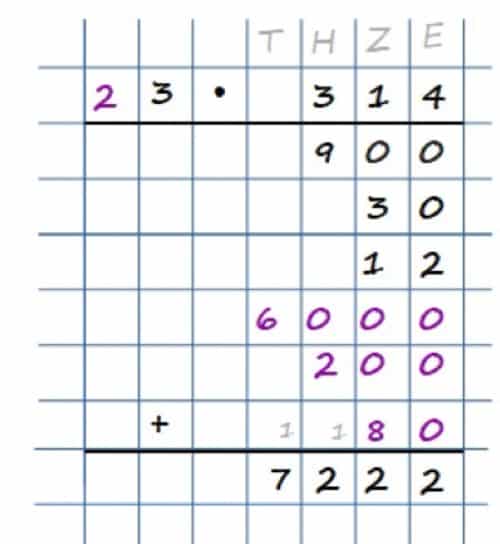
Übrigens:
Beim schriftlich Multiplizieren mit mehreren Stellen kannst Du auch einfach Deine Stellen zählen, um herauszufinden, wie viele Nullen Du hinzufügen musst.
Warum schriftliches Multiplizieren wichtig ist sowie weitere Beispiele zu Möglichkeiten der vereinfachten Multiplikation findest Du in der Übersicht der Universität Duisburg.
Schriftliche Multiplikation Aufgaben
Nun hast Du viel über das Schriftliche Multiplizieren gelernt. Du möchtest das Gelernte vertiefen?In unserem Bereich Schriftliches Multiplizieren Aufgaben kannst Du die Theorie direkt in der Praxis anwenden. Natürlich stellen wir Dir auch die Lösungen der Multiplikationsaufgeben mit einer detaillierten Erklärung und Lösungsweg zur Verfügung.
Übersicht – schriftliches Multiplizieren
Bevor wir zum Ende kommen, möchte ich Dir noch eine Zusammenfassung zur schriftlichen Multiplikation geben, sodass Du nochmal alles in Ruhe überblicken kannst.
Tabelle 1: Eine Übersicht zur schriftlichen Multiplikation
| Multiplikation | Beispiel | Bemerkung |
| Erster Faktor hat eine Stelle/ ohne Überschlag | 3 • 23 | Keine Verschiebung notwendig, da alle Ergebnisse nur eine Ziffer haben |
| Erster Faktor hat eine Stelle/ mit Überschlag | 5 • 123 | Geeignete Verschiebung bzw. Ergänzung von Nullen in den Zwischenergebnissen |
| Beide Faktoren haben mehr als eine Ziffer | 17 • 23 | Wiederhole die obigen Verfahren für jede Ziffer des des jeweiligen Faktors und beachte die Stelle (Einer Zehner usw.) |
Dass schriftliches Multiplizieren eine einfache und schnelle Methode ist, um schnell große Multiplikationsaufgaben zu berechnen, hast Du in diesem Artikel gesehen. Dazu genügt es, den ersten Faktor mit den einzelnen Ziffern des 2. Faktors zu multiplizieren und dabei auf die richtige Stelle (Hunderter, Zehner Einer) zu achten bzw. die richtige Anzahl an Nullen zu ergänzen. Anschließend müssen diese Ergebnisse noch addiert werden. Fertig, nun bist Du ein richtiger Multiplikationsprofi! Im nächsten Schritt solltest Du übrigens schriftliches Dividieren für Dich entdecken.
Literatur
Padberg, Friedhelm; Büchter, Andreas (2015): Einführung Mathematik Primarstufe – Arithmetik. 2. Auflage. Springer, S. 50–55.
Padberg, Friedhelm; Büchter, Andreas (2015): Einführung Mathematik Primarstufe – Arithmetik. 2. Auflage. Springer, S. 50–55.
Knöß, Petra (1989): Fundamentale Ideen der Informatik im Mathematikunterricht: Grundsätzliche Überlegungen und Beispiele für die Primarstufe. Springer, S. 189–201.
FAQs zum Thema schriftlich multiplizieren
Die schriftliche Multiplikation hilft Dir nicht nur, schnell auch große Zahlen miteinander zu multiplizieren. Das Prinzip basiert auf dem so genannten „Distributivgesetz“, das für Dich auch später in der Mathematik eine große Rolle spielen wird. Wenn Dich das neugierig gemacht hat, kannst Du Dich auf der Seite der Universität Heidelberg schon einmal auf dieses Thema einstimmen.
Ja! Genauso wie bei der im Text erwähnten schriftlichen Multiplikation, kannst Du auch Kommazahlen multiplizieren. Dazu musst Du in Deinen Ergebnissen das Komma an die Stelle setzen, an der es auch im 2. Faktor steht. Schau Dir doch als nächstes an, was ungerade Zahlen sind.
Du hast verschiedene Möglichkeiten herauszufinden, ob Deine Multiplikation korrekt ist. Zum Beispiel kannst Du Dein Ergebnis durch einen der beiden Faktoren teilen. Kommt der andere Faktor raus, so hast Du richtig gerechnet. Am schnellsten prüfst Du Dein Ergebnis natürlich mit einem Taschenrechner.
Da Du für die schriftliche Multiplikation kleine Zahlen miteinander multiplizierst, solltest Du Dich mit dem kleinen Einmaleins auskennen. Außerdem benötigst Du die schriftliche Addition, welche Du auch hiermit gut üben kannst.
Diese Art der Multiplikation hilft in erster Linie dabei, große Zahlen auf dem Papier zu multiplizieren. Hierbei übst Du nebenbei aber auch vieles andere, allen voran das Kopfrechnen, was Du immer wieder brauchen wirst!




