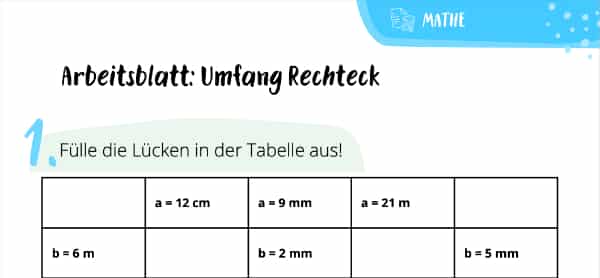
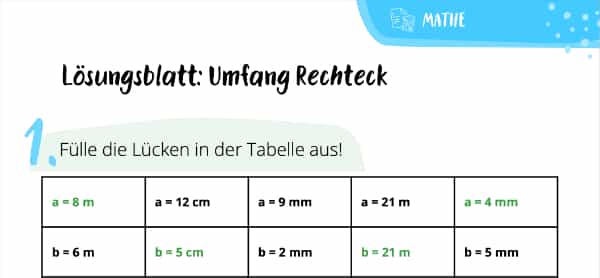
Um den Umfang eines Rechtecks herauszufinden, benötigen wir eine ganz bestimmte Formel. Na, weißt Du, welche das ist? Macht gar nichts, falls Du hierauf noch keine Antwort hast. Denn genau dafür ist dieser Beitrag da! Wir zeigen Dir, mit welcher Formel Du den Umfang von allen möglichen Rechtecken ermittelst. Anschließend testen wir dieses frischgebackene Wissen mit unseren spannenden Übungen und Aufgaben. So kann im nächsten Mathe-Test rein gar nichts schiefgehen!
Der Umfang eines Rechtecks
Um den Umfang (u) einer Figur zu ermitteln, addieren wir einfach seine Seitenlängen. Der Umfang eines Rechtecks tanzt dabei ein wenig aus der Reihe. Weißt Du auch, warum das so ist? Na klar, das liegt an den jeweils zwei gleich langen Seiten des Rechtecks. Wir können es uns daher sparen, jede Seite einzeln in unserer Formel aufzuschreiben. Stattdessen multiplizieren wir je eine davon mit zwei und addieren dieses Produkt mit dem der anderen Seite. Also so:
u = 2 × a + 2 × b
Beispiel gefällig? Wir haben ein Rechteck mit der Seitenlänge a von 11 cm. Die Seite b ist 14 cm lang.
u = 2 × a + 2 × b
u = (2 × 11 cm) + (2 × 14 cm)
u = 50 cm

Arbeitsblätter & Unterrichtsmaterial
So schnell ging das? Einsame Spitze! Dann haben wir ja noch genügend Zeit, um unsere Formel bei ein paar spannenden Übungen auf die Probe zu stellen. Falls Du noch ein wenig Starthilfe benötigst, können wir Dir diese auch jederzeit in der Nachhilfe für die Grundschule geben. Darf es etwas kniffliger sein? Dann schau doch mal bei der Uni Bayreuth vorbei!
Um den Umfang eines Rechtecks zu ermitteln, kannst Du jederzeit auf unsere supereinfache Formel zurückgreifen. Achte aber stets darauf, dass Du wirklich ein Rechteck vor der Nase hast! Ein Trapez lässt sich auf diese Weise zum Beispiel nicht auf den Prüfstand stellen.