Ein Rechteck ist ein regelmäßiges Viereck mit vier rechten Winkeln und jeweils zwei gleich langen Seiten, die einander gegenüber liegen. Doch wie unterscheidet es sich etwa vom Quadrat? Diese Frage werden wir in diesem Beitrag gemeinsam beantworten und uns außerdem ansehen, wie Du den Umfang wie auch den Flächeninhalt dieser geometrischen Figur berechnen kannst. Noch mehr Unterstützung bekommst Du übrigens in der Mathe Nachhilfe.
Rechteck – Definition
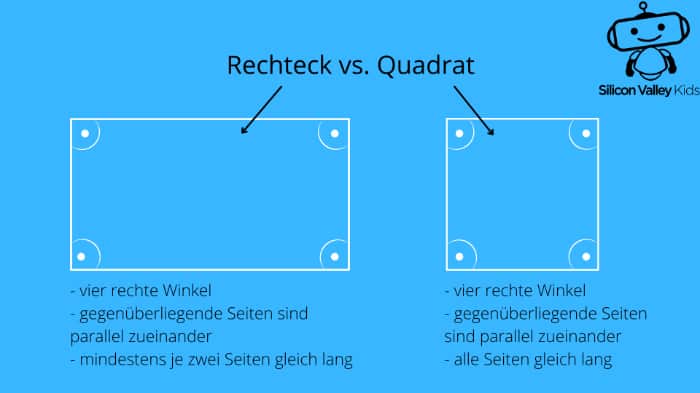
Das Rechteck ist ein regelmäßiges Viereck mit vier rechten Winkeln. Obendrein sind seine gegenüberliegenden Seiten parallel zueinander und gleich lang. Im Gegensatz zum Quadrat müssen nicht alle Seiten identisch sein, sie können aber. Somit ist jedes Quadrat ein Rechteck, aber nicht jedes Rechteck ist ein Quadrat.
Die Eigenschaften des Rechtecks
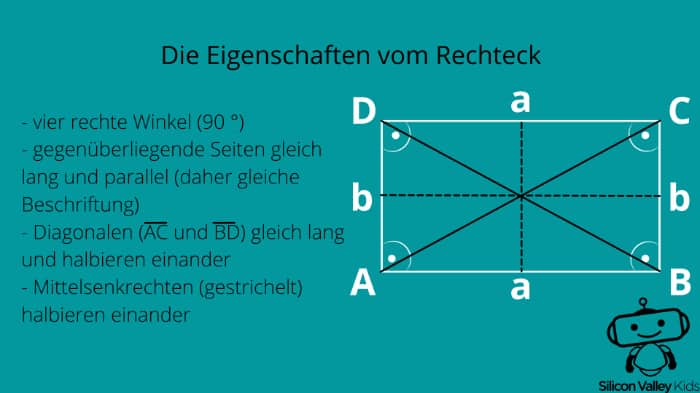
Okay, dann lass uns nochmal etwas genauer auf die Eigenschaften des Rechtecks eingehen! Wir haben bereits festgestellt, dass es vier Ecken und vier gleich große Winkel hat. Genauer gesagt sind seine Winkel 90 ° groß. Man sagt dazu auch rechter Winkel. Zudem sind seine gegenüberliegenden Seiten gleich lang und parallel zueinander. Du beschriftest seine Seiten dementsprechend in der Regel zweimal mit dem kleinen a und zweimal mit b.

Ziehst Du Linien zwischen den gegenüberliegenden Eckpunkten, siehst Du zusätzlich die Diagonalen der Figur. Sie sind ebenfalls genau gleich lang und halbieren einander. Auch die beiden Symmetrieachsen entlang der Mittelsenkrechten halbieren einander, sind aber nicht unbedingt gleich lang. Das ist nur beim Quadrat der Fall.
Flächeninhalt und Umfang berechnen
Kommen wir nun zu dem Teil, der für Dich im Mathe-Unterricht vermutlich am wichtigsten ist: dem Rechnen. Du kannst an einem Rechteck nämlich verschiedene Größen berechnen. Weißt Du, welche das sind? Die Winkel schon mal nicht, die sind ja alle immer 90 ° groß. Dafür kannst Du aber den Umfang und den Flächeninhalt ermitteln. Für die Diagonalen brauchen wir den Satz des Pythagoras, das ist noch etwas zu schwer und wird erst in den weiterführenden Schulen behandelt. Schauen wir uns also lieber an, wie wir den Umfang und den Flächeninhalt berechnen können!
Gewusst?
Sind zwei Linien parallel, bedeutet das, sie werden sich niemals in einem Punkt schneiden (vgl. Sitter, 2019). Selbst dann nicht, wenn Du sie unendlich weiter zeichnen würdest. Wenn Du Dich für solche geometrischen Begriffe interessierst, schau doch mal bei der Uni Frankfurt vorbei!
Umfang
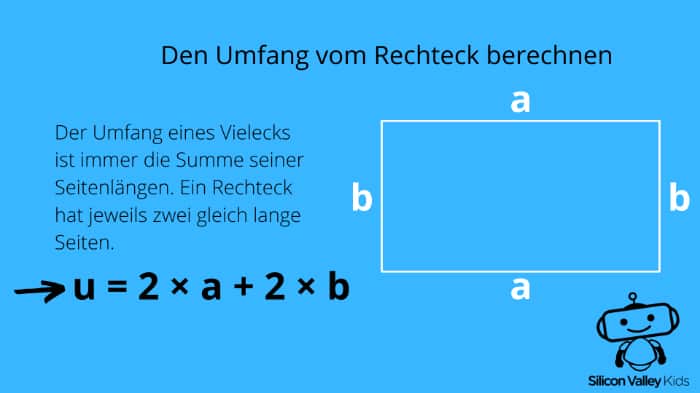
Ein Rechteck gehört zu den Polygenen, also Vielecken, weshalb wir einfach alle Seitenlängen addieren müssen, um seinen Umfang herauszufinden. Du weißt aber ebenfalls bereits, dass die gegenüberliegenden Seiten unserer Figur (a und b) gleich lang sind. Also können wir es uns etwas einfacher machen und einfach zweimal die Länge von a und zweimal die Länge von b addieren. Die Formel für den Umfang (= u) sieht also so aus:
u = 2 × a + 2 × b
Flächeninhalt
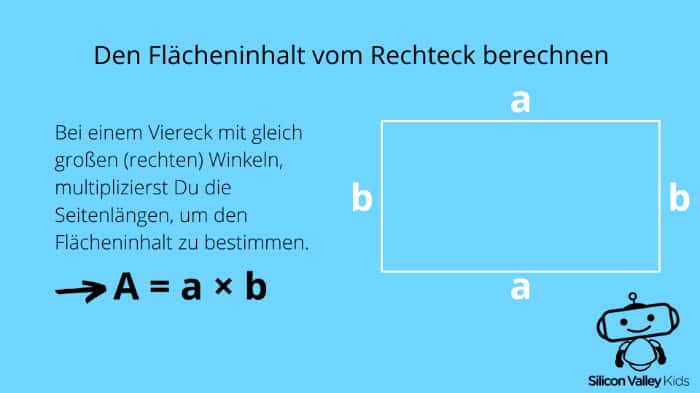
Da das Rechteck vier rechte Winkel hat und zwei Seiten jeweils gleich lang sind, ist die Berechnung seines Flächeninhalts supereinfach! Du multiplizierst nämlich einfach die Seitenlängen der verschieden langen Seiten. Dabei darfst Du nicht vergessen, dass sich die Maßeinheit von Seitenlängen zu Flächen immer verändert. Sie bekommen dann nämlich die Quadratzahl „2“ verpasst. Dadurch werden etwa Millimeter zu Quadratmillimetern (mm2) und Meter zu Quadratmetern (m2). Die Formel zur Berechnung des Flächeninhalts (= A) sieht entsprechend so aus:
A = a × b
Der Vergleich zu anderen Vierecken
Das Rechteck ist ein regelmäßiges Viereck, wozu auch das Quadrat, das Parallelogramm, die Raute, das Trapez und das Drachenviereck gehören. Doch wie unterscheiden sie sich voneinander? Schneid doch mal aus buntem Papier die einzelnen Figuren aus und schau, was das Besondere an ihnen ist! Das klappt auch einwandfrei im Homeschooling. Du kannst Dich dafür an der folgenden Abbildung orientieren.
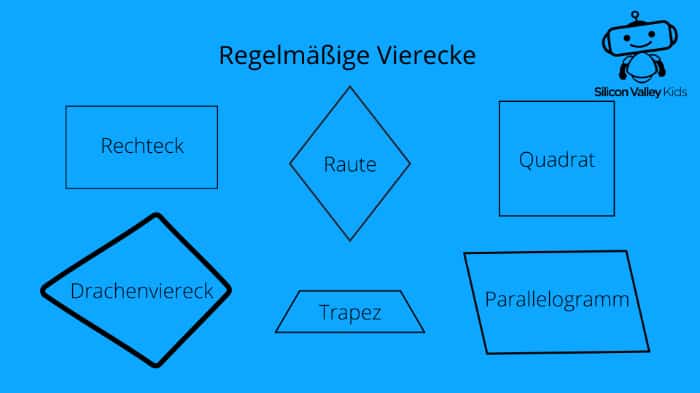
Damit Du auch weißt, worauf Du beim Basteln genau achten musst, stellen wir Dir außerdem die wichtigsten Eigenschaften der Vierecke kurz und knapp vor.
Tabelle 1: Eigenschaften der Vierecke im Vergleich
| Regelmäßiges Viereck | Wichtigste Eigenschaft | Flächeninhalt |
| Rechteck | – vier rechte Winkel | A = a × b |
| Parallelogramm | – jeweils zwei gleich lange und parallele Seiten, außerdem gleich große gegenüber liegende Winkel | A = g × h |
| Quadrat | – vier rechte Winkel und außerdem gleich lange Seiten | A = a2 |
| Trapez | – die zwei gegenüberliegenden Seiten sind parallel zueinander | A = m × h |
| Raute | – ein Parallelogramm, dessen Seiten dabei gleich lang sind | A = a × h |
| Drachenviereck | – die Seiten, die sich an den Symmetrieachsen schneiden, sind gleich lang | A = (e × f) : 2 |
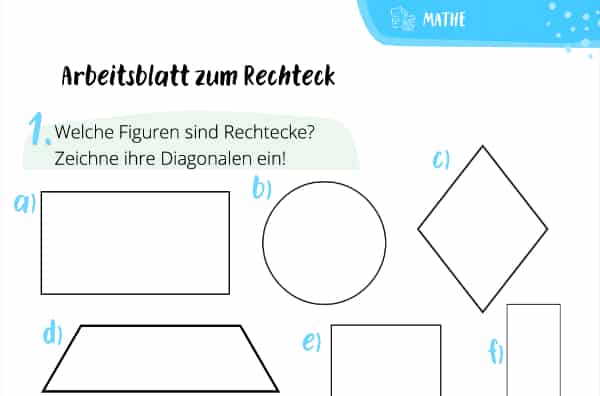
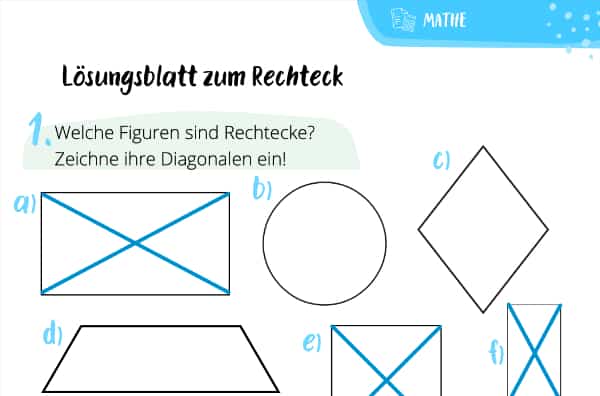
Arbeitsblatt zum Rechteck
Um ein Rechteck zu berechnen, musst Du Dir also im Grunde nur zwei Formeln einprägen. Lass uns doch mal austesten, ob das schon geklappt hat, indem wir uns das folgende Arbeitsblatt vornehmen! Bei Fragen stehen wir Dir aber auch in der Nachhilfe für die Grundschule zur Seite.
So schnell haben wir das Rechteck gemeinsam durchleuchtet! Du weißt nun genau, woran Du es erkennst, wie Du seinen Umfang, aber auch seinen Flächeninhalt berechnest und kannst Dich damit als König:in der Geometrie bezeichnen.
Literatur
Keil, Marion (2010): Lernstationen Mathematik. Geometrische Körper, handlungsorientierter Geometrieunterricht, 1. Auflage Buxtehude.
Sitter, Kerstin (2019): Geometrie in der Grundschule. Geometrische Körper an inner- und außerschulischen Lernorten, Wiesbaden.
FAQs zum Rechteck
Ein Rechteck ist ein regelmäßiges Viereck, das über vier rechte Winkel und jeweils zwei parallele sowie gleich lange Seiten verfügt (vgl. Keil, 2010).
Ja, ein Quadrat erfüllt alle Eigenschaften, die ein Rechteck ausmachen. Denn es hat gleich große Winkel und die gegenüberliegenden Seiten sind parallel wie auch gleich lang. Beim Quadrat sind sogar alle vier Seiten gleich lang. Damit ist jedes Quadrat ein Rechteck, andersrum aber nicht.
Das kann es haben, wodurch es gleichzeitig ein Quadrat wäre, aber es gibt auch Rechtecke, die nur jeweils zwei gleich lange Seiten haben.
Die Formel lautet: u = 2 × a + 2 × b. Bist Du jedoch schon in einer höheren Klassenstufe, sind die spannenden Aufgaben der Uni Bonn zu kongruenten Rechtecken womöglich genau das Richtige für Dich.
Dafür multiplizierst Du einfach die verschieden langen Seiten miteinander. Die Formel sieht dementsprechend so aus: A = a × b.