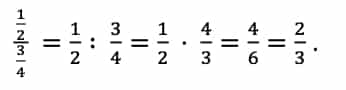Brüche dividieren

Im Alltag kommt es oft vor, dass Du Brüche dividieren möchtest. Das musst Du nämlich können, wenn Du eine Pizza oder Saftschorle gerecht unter Freunden aufteilen möchtest. Damit Du diese Aufgaben als Rechenprofi meisterst, zeige ich Dir nun Schritt für Schritt, wie leicht man Brüche teilen kann. Falls Du noch Hilfe brauchst, erklären wir Dir gern alle wichtigen Rechenregeln in unserer Mathe Nachhilfe.

Inhaltsverzeichnis

Brüche dividieren im Alltag
Wichtige Grundlagen zum Thema Bruch dividieren
- Arten von Brüchen
- Voraussetzungen für das Dividieren von Brüchen
Wie kann man zwei Brüche teilen?
Kehrwert bilden
Dividieren von Brüchen nach Kehrwertbildung
Division von echten Brüchen
Unechte Brüche geteilt rechnen
Dezimalbrüche dividieren
Brüche dividieren mit ganzen Zahlen
Einen gemischten Bruch dividieren
Bruchrechnung Division – eine Übersicht
Brüche dividieren Aufgaben
Literatur
FAQs – Brüche dividieren

Brüche dividieren im Alltag

Brüche dividieren zu können, ist im alltäglichen Leben hilfreich. Es ermöglicht Dir nämlich, viele Alltagsprobleme zu lösen (vgl. Padberg, 2017). Deswegen möchten wir Dir nun einige anschauliche Beispiele für Situationen zeigen, die Du sicher auch schon erlebt hast.

Hast Du zum Beispiel schon einmal einen halben Apfel oder $\frac 3 {4}$ einer Tafel Schokolade gerecht geteilt? Dann hast Du bereits Erfahrung mit dem Teilen von Brüchen. Doch nicht immer ist diese Aufteilung möglich, indem man den Apfel mit einem Messer teilt oder die Würfel der Tafel Schokolode zählt und dann abbricht.

Lernvideo: Brüche dividieren

Auf der unteren Abbildung siehst Du $\frac 3 {4}$ eines übrig gebliebenen Schokokuchens, welcher unter zwei Geschwistern aufgeteilt wurde.

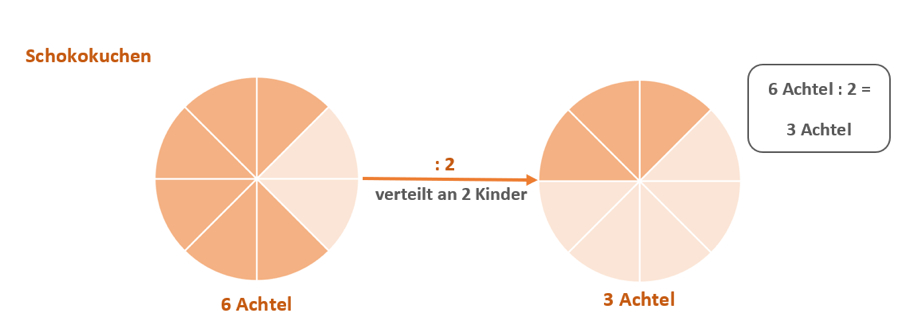
Abb. 1: Brüche dividieren im Alltag

Wie Du diese Aufgaben lösen kannst, erkläre ich Dir später beim Rechnen mit ganzen Zahlen. Zunächst wollen wir aber mit den Grundlagen beginnen, die Du für die Division von Brüchen benötigst. Du hast noch Fragen? Weitere anschauliche Erklärungen findest Du in unserer Rubrik Hausaufgabenbetreuung.

Wichtige Grundlagen zum Thema Bruch dividieren

Falls Du Brüche dividieren willst, musst Du das kleine Einmaleins können und wissen, wie man mal rechnet. Schriftliches Dividieren ist hingegen insbesondere für die Dezimalbrüche wichtig. Ferner gebe ich Dir in den nächsten Abschnitten die wichtigsten Grundlagen an die Hand, damit Du mit dem Dividieren gut zurechtkommst. Da wir mit unterschiedlichen Arten von Bruchzahlen rechnen, möchte ich Dir diese schnell vorstellen.

Erklärvideo: Brüche dividieren – Übungsaufgaben

Arten von Brüchen

Brüche sind Teil eines Ganzen und habe einen Zähler (oberhalb des Bruchstrichs) und einen Nenner (unterhalb des Strichs). Je nachdem, ob der Zähler kleiner oder größer ist als der Nenner, bezeichnet man sie auch als echt oder unecht.

Info:

Man unterscheidet folgende Arten von Brüchen:

Echte (Zähler kleiner als Nenner): $\frac 1 {6}$

unechte (Zähler größer als Nenner oder gleich groß): $\frac 8 {2}$

gemischte (ganze Zahl und ein Bruch): 4 $\frac 1 {2}$

Dezimalbrüche: 0,125

Du kannst sie kürzen, erweitern und umwandeln. Um die Division der Brüche einfacher durchführen zu können, muss man einen gemischten dabei vor dem Rechnen meist in einen unechten umwandeln.

Solltest Du mehr über die verschiedenen Arten wissen wollen, schau Dir das Wissensmagazin auf der Webseite der Universität Tübingen an.

Lernvideo: Kniffelige Rechenaufgaben

Voraussetzungen für das Dividieren von Brüchen

Wenn Du Brüche dividieren möchtest, musst Du wissen, wie Du mit ihnen mal rechnest. Solltest Du dieses Thema nochmal ausführlich wiederholen wollen, lies Dir am besten unseren Artikel Brüche multiplizieren durch. Möchtest Du Dich erst mit den Grundlagen beschäftigen? Dann solltest Du üben, wie schriftliches Multiplizieren funktioniert.

Merke:

Du rechnest mal, indem Du jeweils die beiden Zähler und die beiden Nenner malnimmst: ZÄHLER mal ZÄHLER und NENNER mal NENNER.

Aufgabe:

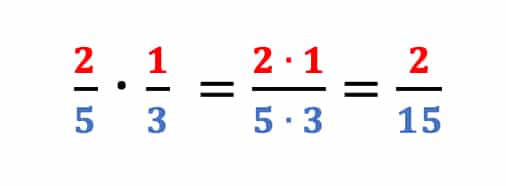
Hier haben wir zunächst Zähler mal Zähler miteinander malgenommen, also 2 und 1. Dann folgten die Nenner: 5 und 3.

Wie kann man zwei Brüche teilen?

Warum Du schon gut mal rechnen können solltest, erkläre ich Dir im nächsten Abschnitt genauer. Zuerst schauen wir uns an, was es bedeutet, Brüche aufzuteilen.

Weißt Du noch?

Erinnerst Du Dich noch an die Division von ganzen Zahlen? Da haben wir uns auch gefragt, wie oft eine Zahl in eine andere Zahl passt. Die Aufgabe 6 : 2 = 3 hat Dir gesagt, dass die 2 genau 3 mal in die 6 passt.

Ebenso wie bei der Division mit ganzen Zahlen, schauen wir nun auch beim Dividieren von Brüchen, wie oft ein Teil in einen anderen passt. Stell Dir vor, dass Du zwei Pizzen vor Dir hast und prüfst wie oft die 2 lila Pizzastücke (Pizza Hawaii) in die grünen Pizzastücke (vegetarische Pizza) passen. Das ist auch eine gute Aufgabe, falls Du schriftliches Subtrahieren üben willst.

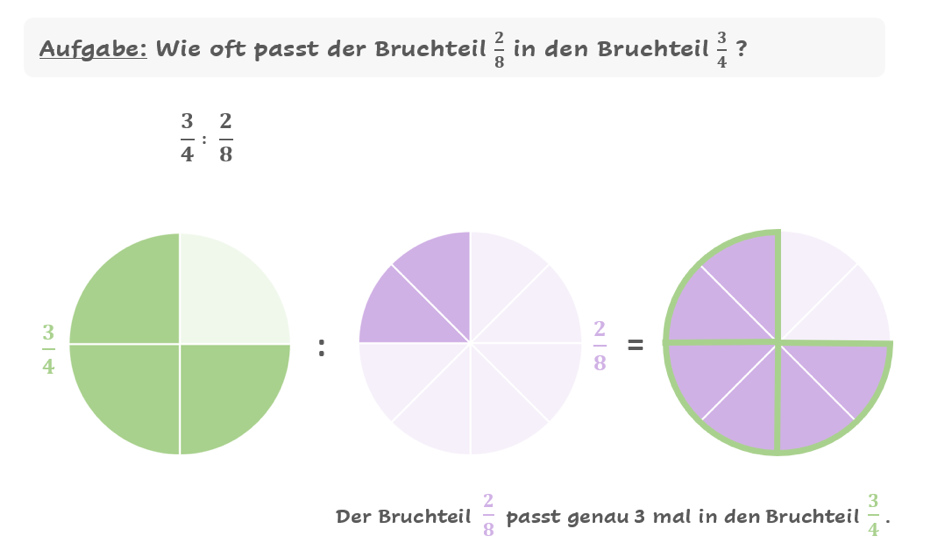
Brüche teilen: Vergleich der Bruchstücke

Abb. 2: Bevor wir die Brüche dividieren, vergleichen wir die Teile

Verschiebe den $\frac 2 {8}$ Teil so, dass er auf die Fläche von $\frac 3 {4}$ passt.

Es passen genau 3 von den $\frac 2 {8}$ -Teilen in die $\frac 3 {4}$ -Teile. Somit lautet die Rechnung: $\frac 3 {4} : \frac 2 {8} = 3$

Kontrollaufgabe: $\frac 2 {8} \cdot 3 = \frac 2 {8} \cdot \frac 3 {8} = \frac 6 {8} = \frac 3 {4}$

Du hast sicherlich gemerkt, dass aus $\frac 2 {8}$ nach dem Kürzen $\frac 1 {4}$ wird. Somit könnte man auch fragen, wie oft passt $\frac 1 {4}$ in $\frac 3 {4}$ .

Du möchtest noch tiefer in das Thema einsteigen? Dann sieh Dir die Informationen der Universität Erlangen an.

Kehrwert bilden

Allerdings passt ein Teil nicht immer so perfekt in einen anderen wie bei unserer Aufgabe oben. Deshalb möchten wir nun lernen, wie man Brüche mithilfe einer Rechnung teilt. Sicherlich fragst Du Dich schon, warum es so wichtig ist, dass Du Bruchzahlen schon gut mal rechnen kannst, bevor Du damit beginnst sie zu teilen. Das verrate ich Dir jetzt! Denn wir verwandeln die Divisionsaufgabe in eine Malaufgabe. Dafür müssen wir den Kehrwert bilden.

Kehrwert bilden

Um den Kehrwert zu bilden, drehe den zweiten Bruch (Divisor) um, indem Du Zähler und Nenner vertauschst. Der Kehrwert von $\frac 1 {4}$ ist $\frac 4 {1}$

Dividieren von Brüchen nach Kehrwertbildung

Nachdem Du den Kehrwert gebildet hast, können wir mit dem Rechnen beginnen. Der erste Bruch bleibt, wie er ist. Nachdem Du den Kehrwert des Zweiten gebildet hast, musst Du die beiden Zahlen miteinander malnehmen. Hierfür rechnest Du wieder Nenner mal Nenner und Zähler mal Zähler.

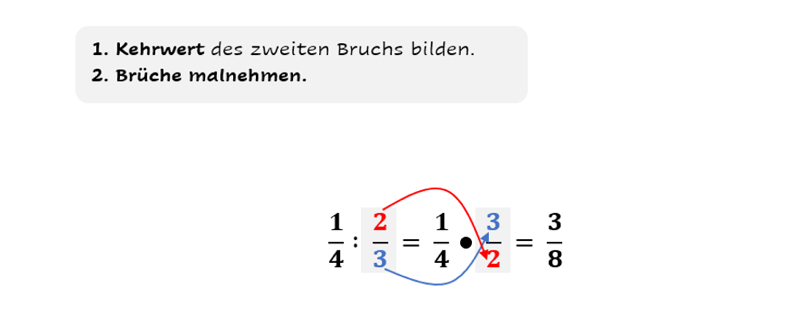
Abb. 3: Wenn wir Brüche dividieren, rechnen wir mit dem Kehrwert

Merke:

Du dividierst durch einen Bruch, indem Du den Ersten mit dem Kehrwert des Zweiten malnimmst: $\frac 1 {8} : \frac 2 {3} = \frac 1 {8} \cdot \frac 3 {2} = \frac {3} {16}$

Division von echten Brüchen

Nun möchten wir noch ein weiteres Beispiel durchgehen, bei welchem wir echte Brüche dividieren. Du erinnerst Dich sicher noch, dass bei diesen der Zähler kleiner ist als der Nenner.

Aufgabe:

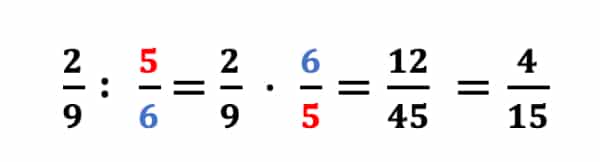
Zuerst bilden wir wieder den Kehrwert von $\frac 5 {6}$ und rechnen dann den ersten Bruch mit dem Zweiten mal. Hierfür rechnen wir Zähler mal Zähler (2 ∙ 6) und Nenner mal Nenner (9 ∙ 5). Somit erhalten wir $\frac {12} {45}$ und können mit 3 kürzen, indem wir den Zähler und den Nenner durch 3 dividieren: 12 : 3 = 4 und 45 : 3 = 15. Das Ergebnis ist $\frac {4} {15}$ .

Kürzen:

Zähler und Nenner werden durch die gleiche Zahl dividiert: $\frac 3 {6} = \frac 1 {2}$

Unechte Brüche geteilt rechnen

Nachdem Du bereits gesehen hast, wie man echte Brüche dividieren kann, wollen wir uns einmal den unechten widmen. Diese haben eine größere Zahl als Zähler als der Nenner: $\frac 7 {3}$ . Um das Dividieren zu vereinfachen, solltest Du immer prüfen, ob Du kürzen kannst.

Übrigens:

Kürze erst, wenn Du die Malaufgabe gebildet hast. Wenn Du mal rechnest, kannst Du nicht nur den Zähler und den Nenner des gleichen Bruchs kürzen, sondern auch über kreuz.

Aufgabe:

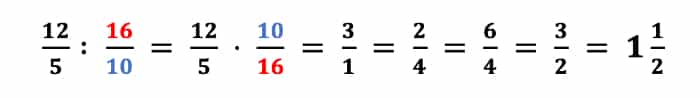
Sobald Du den Kehrwert gebildet und die Divisionsaufgabe in eine Malaufgabe umgewandelt hast, kannst Du kürzen. Kürze die 12 und die 16 mit 4 und die 10 und die 5 mit 5. Danach kannst Du $\frac 2 {4}$ weiter zu $\frac 1 {2}$ kürzen oder das Ergebnis ermitteln und anschließend $\frac 6 {4}$ zu $\frac 3 {2}$ kürzen. Das Ergebnis ist ebenfalls ein unechter Bruch, den Du nun in einen gemischten umwandeln kannst.

Achtung:

Teile den Zähler durch den Nenner, um einen unechten Bruch in einen gemischten umzuwandeln.

Dezimalbrüche dividieren

Um einen Dezimalbruch durch eine natürliche Zahl zu teilen, musst Du Dir das Komma wegdenken.

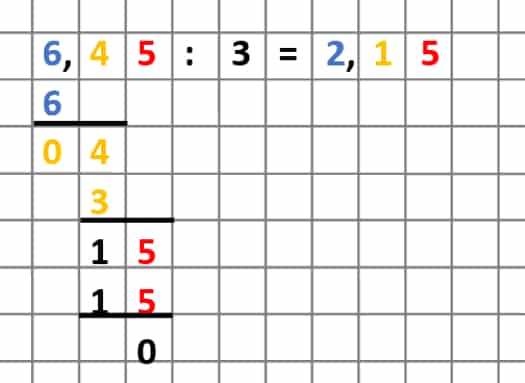
Abb. 4: Dezimalbrüche dividieren

Wenn Du zwei Dezimalbrüche dividieren möchtest, musst Du einen Rechentrick anwenden und die Aufgabe so ändern, dass Du den Dezimalbruch durch eine natürliche Zahl dividieren kannst.

Aufgabe: 0,045 : 0,09

Ändere die zweite Zahl (Divisor) so, dass sie kein Komma mehr hat, indem Du beide Zahlen mit 100 mal nimmst. Somit erhältst Du 4,5 : 9. Jetzt kannst Du die Dezimalbrüche dividieren.

Merke:

Dezimalbruch : Dezimalbruch. Wandle den Divisor zunächst in eine natürliche Zahl um.

Brüche dividieren mit ganzen Zahlen

Nun möchten wir beim Dividieren von Brüchen die ganzen Zahlen jedoch nicht auslassen und durch eine ganze Zahl teilen.

Kehrwert einer ganzen Zahl

Der Kehrwert der Zahl 2 = $\frac 2 {1}$ ist $\frac 1 {2}$

Du erinnerst Dich vielleicht noch an unsere Schokokuchenaufgabe, bei welcher $\frac 6 {8}$ der Torte an 2 Kinder aufgeteilt wurden.

Nun möchten wir für diese Aufgabe eine Rechnung aufstellen:

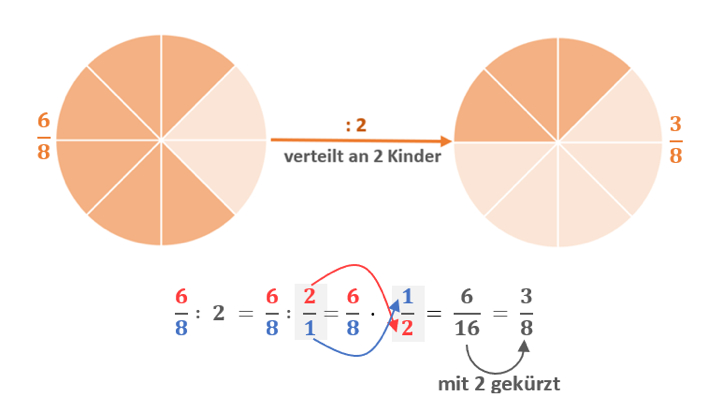
Abb. 5: Durch ganze Zahl teilen

Wir können aber nicht nur einen Bruch durch eine ganze Zahl teilen, das geht zudem auch umgekehrt.

Merke:

Du kannst Brüche mit einer natürlichen Zahl dividieren, indem Du den Nenner mit der natürlichen Zahl mal rechnest und den Zähler beibehältst.

Aufgabe:

Du hast 5 Liter Saftschorle und möchtest diese auf Gläser mit einem Fassungsvermögen von $\frac 1 {3}$ an aufteilen. Wie viele Gläser kannst Du füllen?

Rechnung:

$5: \frac 1 {3} = \frac 5 {1} : \frac 1 {3} = \frac 5 {1} \cdot \frac 3 {1} = 15$

Lösung: Demnach kannst Du 15 Gläser mit Saftschorle füllen.

Hast Du Dich übrigens schon über die Ergebnisse bei der Division von Brüchen gewundert? Viele Schüler staunen bei den Lösungen, denn sie sind es gewohnt, dass die Ergebnisse beim Dividieren kleiner werden (vgl. Prediger, 2004). Schließlich kennt man es so von 6 : 3 = 2. Doch bei der Bruchrechnung ist dies nicht mehr der Fall. Also haben wir richtig gerechnet!

Einen gemischten Bruch dividieren

Du kannst jetzt echte und unechte Brüche dividieren und hast gelernt, wie man sie durch eine ganze Zahl teilt. Nun schauen wir uns noch an, wie man gemischte Brüche dividieren kann.

Bevor Du mit dem Dividieren beginnst, musst Du den gemischten Bruch in einen unechten umwandeln.

Merke:

Um einen gemischten Bruch umzuwandeln, rechne Ganze Zahl • Nenner + Zähler.

So dividierst Du mit gemischten Brüchen:

Alle gemischten Brüche zuerst in einen unechten umwandeln.
Kehrwert bilden.
Wandle die Divisionsaufgabe in eine Malaufgabe um.
Kürze wie gewohnt.
Nehme die beiden Bruchzahlen miteinander mal: Zähler • Zähler und Nenner • Nenner.

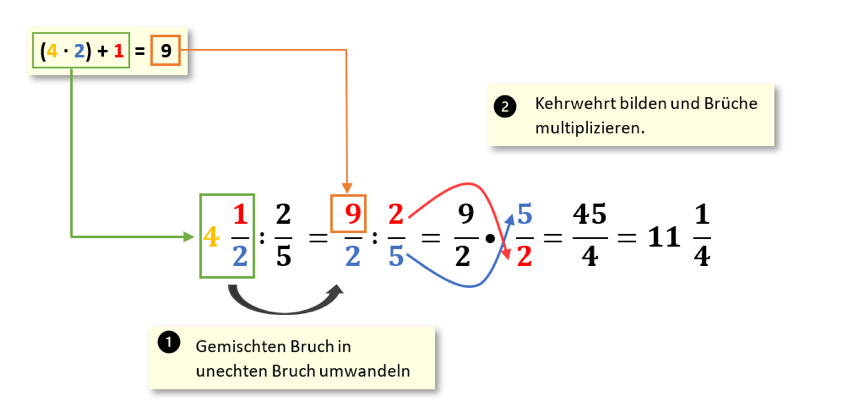
Abb. 6: Wie man gemischte Brüche dividieren kann

Bruchrechnung Division – eine Übersicht

Du weißt jetzt, wie man verschiedene Brüche dividieren sollte. Abschließend findest Du hier eine Tabelle mit allen Rechenarten inklusive Beispielen und Erklärungen.

Tabelle 1: Eine Übersicht zur Division von Brüchen

\frac 1 {5} : \frac 3 {7} = \frac 1 {5} \cdot \frac 7 {3} = \frac 7 {15}

\frac 1 {3} : 4 = \frac 1 {3} \cdot \frac 1 {4} = \frac 1 {12}

Kennst Du übrigens schon das Bruchmärchen? Noch nicht? Dann wird es aber Zeit, dass Du es kennenlernst. Es wird außerdem auch „Das Märchen von dem bösen Drachen und dem klugen Bruch“ genannt. Du kannst es auf Seite 5 einer Veröffentlichung der Universität Dortmund nachlesen.

Brüche dividieren Aufgaben

Nachdem Du viel über das Dividieren von Brüchen erfahren hast, kannst Du mit unseren Aufgaben Dein Wissen vertiefen und üben. Deswegen haben wir Dir einige Übungsaufgaben mit Lösungen und Erklärungen zur Division erstellt. Viel Spaß beim Üben!

Download Arbeitsblatt

Download Lösungen

Brüche zu teilen ist leicht, denn nachdem Du den Kehrwert vom Divisor gebildet hast, musst Du die Zahlen einfach mal rechnen. Du hast außerdem gelernt, wie man echte, unechte, gemischte und Dezimalbrüche dividiert. Mit diesem Wissen kannst Du nun alle Aufgaben problemlos rechnen. Falls Du Dich traust, dann schau nun, wie man Brüche addieren kann.

Literatur

Padberg, F., Wartha, S. (2017): Didaktik der Bruchrechnung. Heidelberg: Elsevier Spektrum Akademischer Verlag.

Prediger, S. (2004): Brüche bei den Brüchen – aufgreifen oder umschiffen. Mathematik lehren, 123, pp. 10-13.

FAQs – Brüche dividieren

Kann man auch drei Brüche dividieren?

Natürlich kannst Du auch drei oder mehrere Brüche teilen. Dafür bildest Du von allen Zahlen, durch die Du dividieren möchtest, den Kehrwert. Danach hast Du eine lange Aufgabe, die auch ungerade Zahlen enthält: $\frac 7 {8} : \frac 1 {2} : \frac 2 {3} = \frac 7 {8} : \frac 2 {1} \cdot \frac 3 {2} = \frac {42} {16} = 2 \frac 5 {8}$ .

Wie funktioniert das Dividieren von Brüchen mit dem gleichen Nenner?

Ebenso kannst Du wie gewohnt Brüche teilen, die gleiche Nenner haben. Bestimmt ist Dir aber schon die Besonderheit aufgefallen, dass die beiden gleichen Zahlen durch Kürzen verschwinden: $\frac 3 {4} : \frac 2 {4} = \frac 3 {4} \cdot \frac 4 {2} = \frac 3 {2}$ .

Was ist ein Doppelbruch und wie kann man diese Bruch dividieren?

Bei einem Doppelbruch sind der Zähler und der Nenner ein Bruch, d.h. Du hast einen auf dem oberhalb und zudem einen unterhalb. Da der Bruchstrich ein Geteiltzeichen ist, kann man beide teilen. Teile den sie, indem Du sie in eine Aufgabe umschreibst:

Wie kann ich Brüche im Kopf dividieren?

Das Dividieren im Kopf fällt Dir leichter, wenn Du vor dem Rechnen kürzt. Dann musst Du anschließend nur noch den Kehrwert bilden und diesen mal rechnen. So kannst Du außerdem gleichzeitig Kopfrechnen üben.

Ist das Plusrechnen oder die Division von Brüchen einfacher?

Wenn Du Brüche dividieren möchtest, bildest Du einfach eine Malaufgabe. Das Plusrechnen ist ein bisschen schwieriger, da Du hier erst einen sogenannten „gemeinsamen Nenner“ finden musst. Wie schriftliches Addieren funktioniert, erklären wir Dir übrigens in einem anderen Artikel.

Division	Beispiel	Bemerkung
2 dividieren	$\frac 1 {5} : \frac 3 {7} = \frac 1 {5} \cdot \frac 7 {3} = \frac 7 {15}$	Kehrwert des Divisors bilden und Zahlen mal rechnen.
Durch ganze Zahl teilen	$\frac 1 {3} : 4 = \frac 1 {3} \cdot \frac 1 {4} = \frac 1 {12}$	Nenner mit der ganzen Zahl mal rechnen und Zähler beibehalten.
Ganze Zahl durch Bruch teilen	$4: \frac 2 {3} = \frac 4 {1} \cdot \frac 3 {2} = \frac {12}{2}$	Nenner mit der ganzen Zahl mal rechnen und Zähler wird Nenner.
Dezimalbrüche	4,5 : 5 = 1,5	Schriftliche Division durchführen und anschließend die Kommastelle ermitteln.
Gemischte	$2 \frac 1 {4} : \frac 1 {3} = \frac 9 {4} : \frac 1 {3} = \frac 9 {4} \cdot \frac 3 {1} = \frac {27}{4}$	Gemischten Bruch in unechten umwandeln. Anschließend den Kehrwert bilden. Dann beides miteinander mal rechnen.