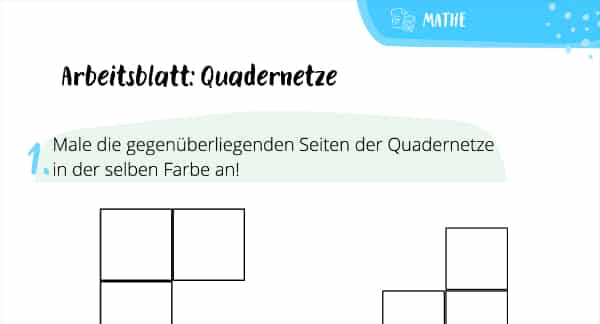
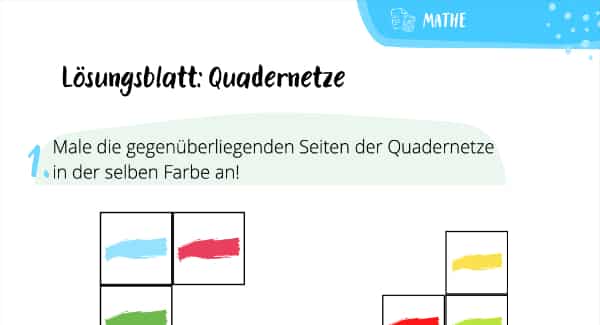
Quadernetze und Kantenmodelle helfen Dir dabei, die wichtigsten Eigenschaften, Gemeinsamkeiten und Unterschiede von Quadern zu erkennen. Ganz nebenbei verbessert sich darüber hinaus Dein räumliches Verständnis. Deswegen reden wir in diesem Beitrag nicht lange um den heißen Brei herum! Stattdessen erklären wir Dir kurz und knapp, was diese beiden Begriffe bedeuten und haben anschließend ein paar tolle Übungen und Aufgaben für Dich im Angebot. Die können wir auch gerne in der Mathe Nachhilfe ins Visier nehmen.
Quadernetze und Kantenmodell – Definition
Stell Dir einmal vor, Du würdest einen Quader so abrollen, dass all seine Teilflächen in einer Ebene liegen. Das nennt sich dann Quadernetz. Wenn Du die Kanten der Teilflächen dieses Quadernetzes wieder entsprechend knickst, entsteht hingegen der dreidimensionale Quader.
Bei einem Kantenmodell wird der geometrische Körper hingegen nur durch die ihn begrenzenden Kanten dargestellt. Quadernetze und Kantenmodell helfen Dir dabei, wichtige Gemeinsamkeiten und Unterschiede von Quadern und Würfeln zu erkennen. Es gilt bei diesen beiden Körpern aber stets, dass zwei Flächen aufeinandertreffen und drei Kanten eine Ecke bilden. Die Kanten stehen hier außerdem immer im rechten Winkel zueinander.

Arbeitsblätter und Übungen
Quadernetze und Kantenmodelle schulen Dein räumliches Denken und helfen Dir dabei, die Eigenschaften dreidimensionaler Körper besser zu verstehen. Lass uns also direkt mit der einen oder anderen Übungsaufgabe dazu starten! Hilfe bekommst Du dabei jederzeit in der Nachhilfe für die Grundschule. Noch mehr Aufgaben findest Du übrigens bei der Uni Bayreuth.
Manchmal muss man ein wenig nachdenken, um bei Quadernetzen und Kantenmodellen den Durchblick zu behalten. Nimm Dir die Zeit, die Du dafür benötigst! Früher oder später macht es dabei immer Klick und Du hast den vollen Durchblick. Wir glauben ganz fest an Dich!
FAQs – Quadernetze & Kantenmodell
Ein Quadernetz entsteht durch das Abrollen der Seitenflächen eines Quaders auf eine flache Ebene. Dabei gibt es insgesamt 54 Möglichkeiten. Alle 54 Quadernetze eines Quaders bilden am Ende ein- und denselben geometrischen Körper.
Bei einem Kantenmodell wird der Quader, Würfel oder ein anderer geometrischer Körper nur durch die ihn begrenzenden Flächen dargestellt. Dadurch erkennt man ganz genau, wie viele Kanten es gibt, wie sie aufeinandertreffen und wie viele Kanten eine Ecke ergeben.
Das liegt daran, dass bei einem Würfel alle Flächen gleich groß und die Kanten gleich lang sind. Bei einem Quader ergeben sich mehr entsprechende -netze, da es verschieden große Flächen gibt.
Eine quadratische Pyramide hat acht Kanten. Vier gehören zur quadratischen Grundfläche, vier weitere zu den Dreiecksflächen, die zur Pyramidenspitze führen.
Nein, denn ein Quadrat ist eine ebene, also zweidimensionale Figur mit vier gleich langen Seiten und gleich großen Winkeln. Der Quader ist hingegen ein dreidimensionaler Körper, dessen Teilflächen aus Rechtecken bestehen.