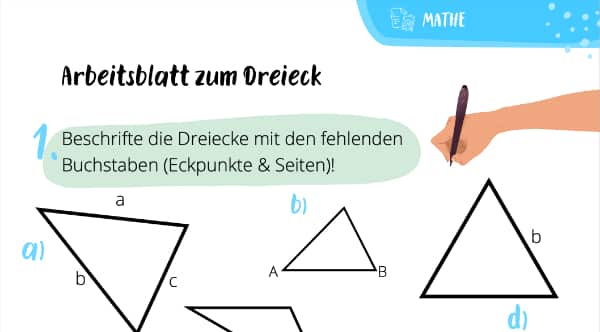
Ein Dreieck ist eine ebene geometrische Figur mit ganz genau drei Ecken, Winkeln und Seiten. Wie lang oder groß diese dabei sind, hängt von der jeweiligen Art ab. Doch wie beschriftet man diese Form eigentlich? Und wie berechnest Du ihren Umfang oder Flächeninhalt? Keine Sorge, all das zeigen wir Dir in diesem Beitrag. Gerne unterstützen wir Dich auch in der Mathe Nachhilfe, falls danach noch Fragen offen sind.
Dreieck – Definition
Das Dreieck ist eine ebene geometrische Figur, die genau drei Ecken, Seiten und Winkel vorzuweisen hat. Das verrät ja auch schon sein Name. Und so kann es dementsprechend aussehen:

So beschriftest Du ein Dreieck
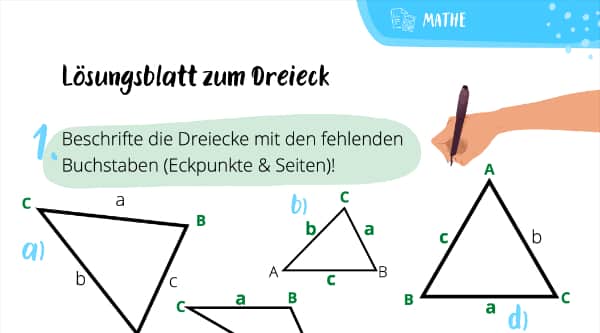
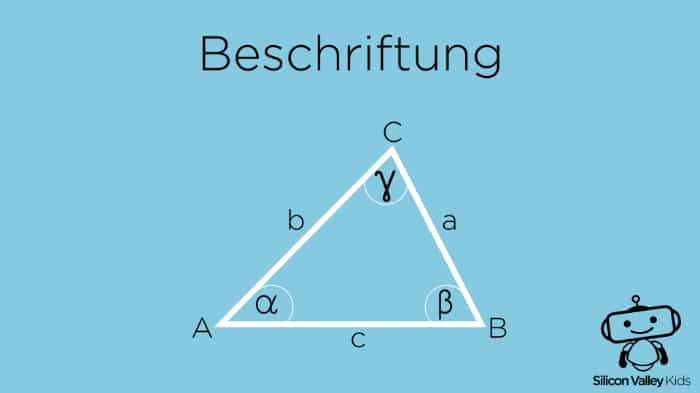
Bei einem Dreieck beschriftest Du die Eckpunkte (A, B und C gegen den Uhrzeigersinn), die gegenüberliegenden Seiten mit den entsprechenden Kleinbuchstaben (a, b und c) und die Innenwinkel mit den griechischen Buchstaben a (bei A), b (bei B) und g (bei C). Schau mal, etwa so:
Diese Linien solltest Du kennen
Neben den drei Seiten gibt es in unserem Dreieck vier wichtige Geraden, die Du kennen solltest. Dazu gehört die Höhengerade, die wir später noch bei der Berechnung des Flächeninhalts brauchen werden. Außerdem gibt es die Mittelsenkrechte, die Seitenhalbierende und die Winkelhalbierende. Von jeder dieser Linien gibt es jeweils drei Stück, die zu den drei Seiten oder Winkeln der Figur gehören. Auf dem folgenden Bild haben wir Dir aber nur jeweils ein Beispiel eingezeichnet, damit es übersichtlich bleibt.

Welche besonderen Dreiecke gibt es?
Manche Dreiecke haben ganz bestimmte Eigenschaften, nach denen sie benannt wurden. Dazu gehören:
- das gleichschenklige Dreieck (zwei Seiten sind gleich lang)
- das gleichseitige Dreieck (alle Seiten sind gleich lang)
- das rechtwinklige Dreieck (ein Winkel ist genau 90 Grad groß, es ist also ein rechter Winkel)

Berechnung
Im Mathe-Unterricht sollst Du ein Dreieck nicht nur erkennen und zeichnen, sondern auch berechnen können. Später musst Du manchmal auch den Schwerpunkt bestimmen, wie es etwa die Uni Siegen vormacht. Aber wir konzentrieren uns hierbei nur auf Umfang und Flächeninhalt, damit es nicht zu schwierig wird.
Umfang
Den Umfang (u) vom Dreieck berechnest Du ganz einfach, indem Du seine drei Seitenlängen addierst. Das heißt also:
u = a + b + c
Flächeninhalt
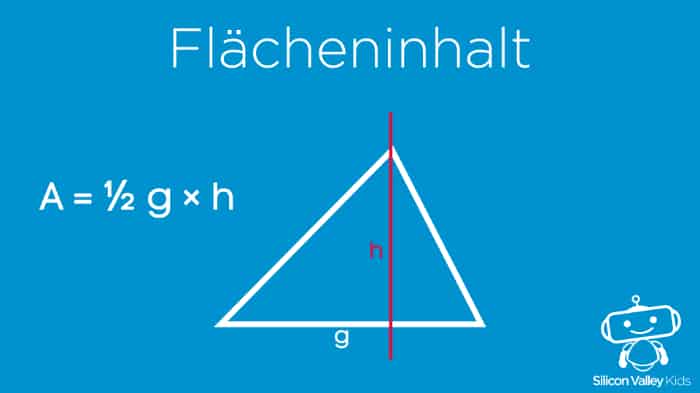
Etwas kniffliger wird es, wenn wir den Flächeninhalt (A) bestimmen wollen. Dafür suchen wir uns eine beliebige Seite aus, die wir hierfür mal kurz in „g“ umbenennen. Nun brauchen wir außerdem die Höhe „h“ dieser Seite. Sie steht dabei im rechten Winkel zu g und führt durch den Eckpunkt der gegenüberliegenden Seite. Welche Seite Du hierfür benutzt, ist ganz egal. Und dann multiplizierst Du einfach die Hälfte von g mit der Höhe h.
A = ½ g × h
Übungsaufgaben zum Dreieck
Voll einfach, die Sache mit dem Dreieck, oder? Dann bist Du jetzt sicher bereit für ein paar coole Übungsaufgaben. Rückendeckung geben wir Dir dabei auch gerne in der Nachhilfe für die Grundschule.
Ein Dreieck ist eine superwichtige geometrische Figur, die Dir im Alltag, aber auch im Mathe-Unterricht ständig begegnet. Doch da Du mittlerweile Expert:in auf diesem Gebiet bist, ist das natürlich gar kein Problem. Und falls Du doch nochmal schmulen musst, wenn es um Fläche und Umfang geht, kannst Du jederzeit zu uns zurückkehren. Wir sagen‘ s auch garantiert nicht weiter.
Literatur
Hilbert, David (2013): Grundlagen der Geometrie, 13. Auflage Stuttgart.
Trill-Zimmermann, Monika (2014): Kopfgeometrie. Von der Handlung in den Kopf.