Ein Quadrat ist ein Viereck mit vier rechten Winkeln und genau gleich langen Seiten. Es ist somit eine ganz besondere Art des Rechtecks, das bestimmte Merkmale mit sich bringt. Diesen kommen wir in diesem Beitrag gemeinsam auf die Spur! Außerdem lernen wir, wie man den Umfang oder den Flächeninhalt einer solchen Figur berechnet. Das testen wir dann auch gleich an einem coolen Arbeitsblatt aus. Falls Du dabei noch Hilfe benötigst, unterstützen wir Dich zusätzlich gerne in der Mathe Nachhilfe.
Quadrat – Definition
Ein Quadrat ist ein Rechteck mit vier gleich langen Seiten. Es hat also vier rechte Winkel (90°), was bedeutet, dass die benachbarten Seiten senkrecht zueinanderstehen. Durch die identischen Winkel und Seitenlängen zählen wir es obendrein zu den regelmäßigen Vierecken. In diesem Sinne ist das Quadrat sogar das regelmäßigste Viereck, das wir haben, da etwa das Drachenviereck nur zwei gleich große Winkel und jeweils zwei gleich lange Seiten vorzuweisen hat.
Eigenschaften des Quadrats
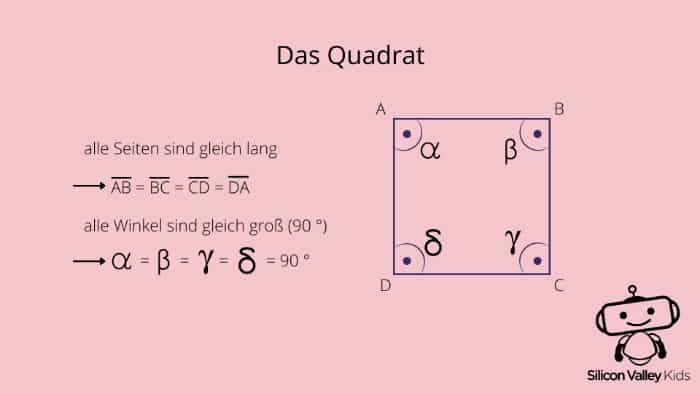
Einige Eigenschaften vom Quadrat haben wir uns ja schon angeschaut. Zum einen hat es vier gleich große Winkel, die allesamt 90° betragen. Man sagt dazu auch „rechter Winkel“. Ebenso sind die vier Seiten dieser Figur exakt gleich groß. Das macht es auch so besonders im Vergleich zum Rechteck im Allgemeinen. Bei einem Rechteck müssen zwar auch die Winkel gleich groß sein, aber nicht die Seiten.
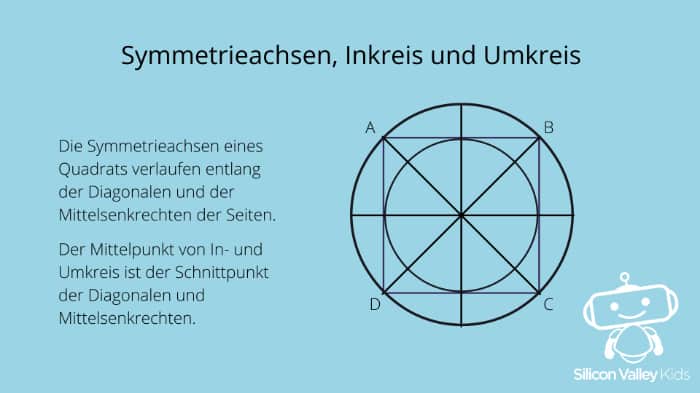
Welche Merkmale hat es noch? Unser gleichseitiges Rechteck ist sowohl achsen- als auch punktsymmetrisch. Die Achsensymmetrie bedeutet, dass Du es an vier Symmetrieachsen spiegeln kannst. Diese Achsen (die beiden ebenfalls gleich langen Diagonalen und Mittelsenkrechten) führen dabei allesamt durch den Mittelpunkt des Quadrats. Würdest Du es am Mittelpunkt einmal um 180° drehen, würde die Figur außerdem genauso aussehen wie davor. Und damit ist es punktsymmetrisch.
Und zu guter Letzt hat unsere Figur einen Inkreis und einen Umkreis, deren Mittelpunkt mit dem Schnittpunkt der Diagonalen identisch ist.
So berechnest Du es
Das Quadrat ist neben dem Viereck allgemein und dem Rechteck eine der ersten geometrischen Figuren, die Du in der Schule kennenlernst (vgl. Bruns et al., 2021). Im Mathe-Unterricht wird von Dir dabei nicht nur erwartet, dass Du es erkennst, sondern auch berechnen kannst. Zu den wichtigsten Größen, die bei dieser Figur ermittelt werden können, gehören der Umfang, Flächeninhalt, die Diagonalen und die Seitenlängen. Weil wir für das Berechnen der Diagonalen und Seitenlängen aber die Rechenoperation „Wurzelziehen“ benötigen und Du das erst in der Oberschule lernst, schauen wir uns hier nur den Umfang und den Flächeninhalt an!

Umfang
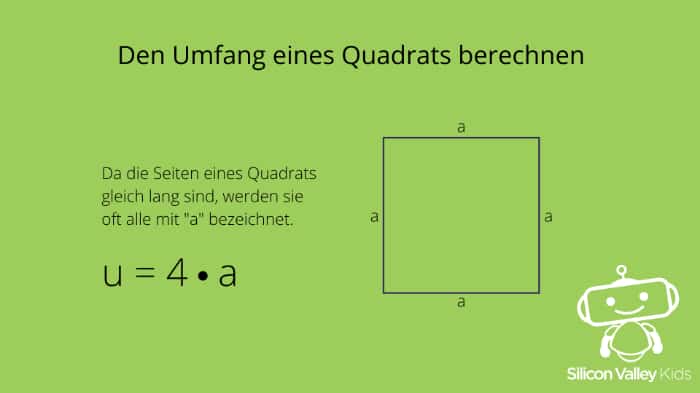
Lass uns mal überlegen, wie wir den Umfang (= u) des Quadrats berechnen können! Zunächst einmal: Der Umfang eines Vielecks ist die Summe all seiner Seitenlängen. Ein Quadrat ist ein Vieleck, also könnten wir einfach seine vier Seiten addieren. Aber halt mal! Erinnerst Du Dich, dass unsere Figur vier gleich lange Seiten hat? Dann können wir ja auch einfach die Länge einer Seite mit 4 multiplizieren! Die Einheit der Seitenlänge verändert sich dabei nicht. Die Formel dazu sieht also so aus:
u = 4 × a
Flächeninhalt
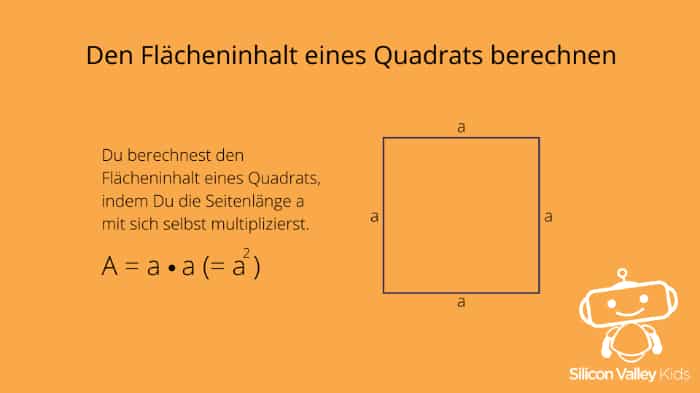
Doch wie berechnen wir nun den Flächeninhalt (= A) eines Quadrats? Du weißt vielleicht schon, dass Du den Flächeninhalt eines Rechtecks herausfindest, indem Du den Wert der unterschiedlich langen Seiten miteinander multiplizierst. Du rechnest also: a × b. Da in einem Quadrat alle Seiten gleich lang sind, rechnest Du dementsprechend: a × a (oder auch a2). Die Einheit (also etwa Zentimeter oder Meter) bekommt dabei ebenfalls die Quadratzahl „2“ verpasst. Aus Zentimetern werden also Quadratzentimeter (cm2) und aus Metern Quadratmeter (m2). Das kennst Du vielleicht schon aus der Hausaufgabenbetreuung.
A = a × a (oder a2)
Vierecke im Vergleich
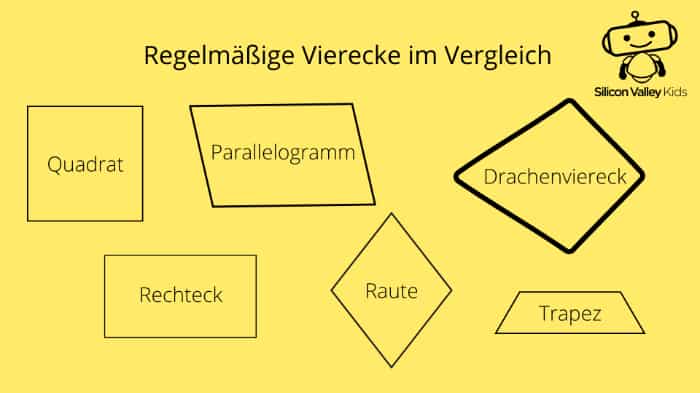
Du hast sicher schon mitbekommen, dass es neben dem Quadrat noch andere regelmäßige Vierecke gibt. Dazu gehören das Rechteck, das Parallelogramm, die Raute (wobei ein Quadrat immer auch ein Rechteck, eine Raute und ein Parallelogramm ist), das Trapez und das Drachenviereck. Diese kannst Du auch prima im Homeschooling aus buntem Papier ausschneiden und ihre Eigenschaften erforschen. Doch wie unterscheiden sie sich voneinander?
Tabelle 1: Vierecke im Vergleich
| Viereck | Eigenschaften | Umfang |
| Quadrat | – gleich lange Seiten und gleich große Winkel (90 °) | u = 4 × a |
| Rechteck | – vier gleich große Winkel (90 °) | u = 2 × a + 2 × b |
| Parallelogramm | – jeweils zwei Seiten sind gleich lang und parallel zueinander, außerdem sind die gegenüberliegenden Winkel gleich groß | u = 2 × a + 2 × b |
| Raute | – Parallelogramm mit vier gleich langen Seiten | u = 4 × a |
| Trapez | – zwei gegenüberliegende Seiten sind parallel zueinander | u = a + b + c + d |
| Drachenviereck | – die Seiten, die einen Schnittpunkt entlang der Symmetrieachse haben, sind gleich lang | u = 2 × a + 2 × b |
Damit Du Dir das noch ein bisschen besser vorstellen kannst, zeigen wir Dir die fünf regelmäßigen Vierecke nochmal in einem Bild.
Arbeitsblatt: Quadrat
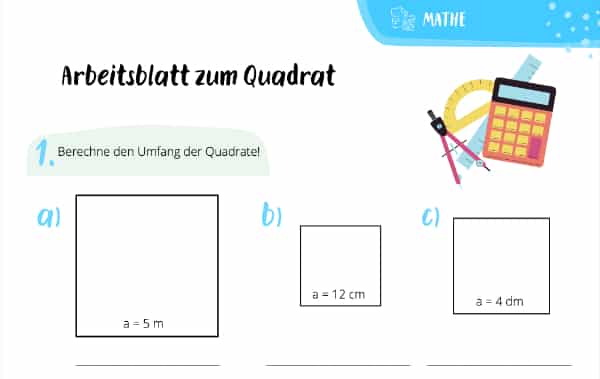
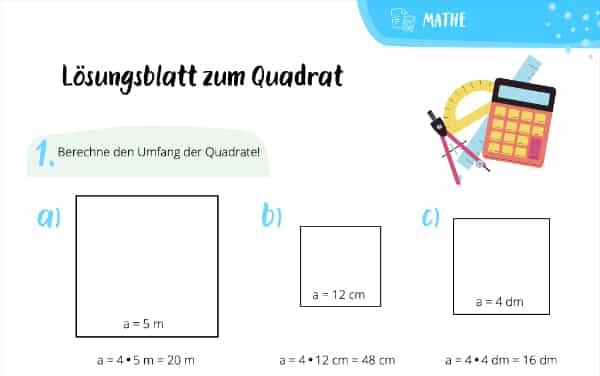
Das war doch total easy peasy, oder? Dann lass uns jetzt schauen, ob Du Dein Wissen auch in die Tat umsetzen kannst. Dafür haben wir ein cooles Arbeitsblatt vorbereitet, mit dem Du den Umfang und den Flächeninhalt verschiedener gleichseitiger Rechtecke berechnen kannst. Los geht‘ s!
Das war‘ s schon? Tatsächlich! So schnell sind wir unserem Quadrat auf die Schliche gekommen. Du weißt nun ganz genau, wie Du dieses besondere Viereck erkennst, seine Größen berechnest und es zum Beispiel vom Drachenviereck unterscheiden kannst. Der nächste Geometrie-Test wird also ein Klacks! Falls Du aber noch ein wenig Hilfe benötigst, sind wir in der Nachhilfe für die Grundschule jederzeit für Dich da.
Literatur
Bruns, Julia et al. (2021): Geometrisches Begriffsverständnis in der Grundschule am Beispiel der Begriffe Viereck, Rechteck und Quadrat.
Roth, Jürgen (2009): Quadrate erforschen. Mathematik an Konkreter Kunst entdecken.
FAQs zum Quadrat
Ein Quadrat ist ein Rechteck mit vier gleich großen Winkeln (90 °) und vier gleich langen Seiten. Es ist außerdem achsen- und punktsymmetrisch. Damit ist es das Viereck mit den meisten Symmetrieeigenschaften (vgl. Roth, 2009).
Jedes Quadrat ist ein Rechteck, da ein Rechteck ein Viereck mit vier rechten Winkeln ist. Das trifft dabei auf jedes Quadrat zu. Aber nicht jedes Rechteck ist ein Quadrat, da ein Rechteck auch jeweils zwei verschieden lange Seiten haben kann.
Ja, das ist möglich, da ein Parallelogramm jeweils zwei zueinander parallele Seiten hat. Und das ist bei einem Quadrat ja auch der Fall. Nur müssen die Winkel eines Parallelogramms nicht zwangsläufig 90 ° groß und die Seiten nicht gleich lang sein. Damit ist jedes Quadrat auch ein Parallelogramm, aber nicht jedes Parallelogramm ist auch ein Quadrat.
Es gibt Rechtecke, Parallelogramme und Rauten, die auch Quadrate sind. Diese müssen dann aber auch die besonderen Eigenschaften (gleich große Winkel und gleich lange Seiten) erfüllen. Tolle Denkspiele zu diesem Thema gibt es übrigens bei der Uni Bielefeld.
Dafür musst Du einfach die Seitenlänge (alle vier Seiten sind identisch groß) mit sich selbst multiplizieren. Die Formel lautet also „A = a × a (oder a2)”. Ein tolles Erklärvideo dazu gibt es auch bei der Uni Luxembourg.