
Brüche multiplizieren ist nicht schwer. Da Bruchzahlen Dir überall im Alltag begegnen können, musst Du manchmal mit ihnen rechnen. Damit Du diese Alltagsprobleme gut meisterst, zeige ich Dir deshalb, wie einfach das Multiplizieren von Brüchen ist. Dabei begleite ich Dich Schritt für Schritt durch die Multiplikation der Brüche. Das Einmaleins und schriftliches Multiplizieren solltest Du jedoch bereits können. Falls Du möchtest, zeigen wir Dir das Bruchrechnen auch gerne in unserer Mathe Nachhilfe.
Inhaltsverzeichnis
- Brüche multiplizieren im Alltag
- Grundlagen für das Multiplizieren von Brüchen
- Multiplikation von echten Brüchen
- So funktioniert das Kürzen
- Drei Brüche multiplizieren
- Multiplizieren von unechten Brüchen
- Brüche mal rechnen mit ganzen Zahlen
- Dezimalbrüche multiplizieren
- Gemischte Brüche multiplizieren
- Übersicht – Multiplikation von Brüchen
- Übungsaufgaben zum Multiplizieren von Brüchen
- Literatur
- FAQs – Bruch multiplizieren
Brüche multiplizieren im Alltag
Brüche multiplizieren im Alltag? Bruchzahlen gibt es nicht nur im Mathematikunterricht, sondern überall in Deiner Lebenswelt. Die Bruchrechnung hat eine wichtige Bedeutung für das alltägliche Leben und hilft Dir dabei, Probleme zu lösen (vgl. Padberg, 2017). Zum Beispiel sieht man bei Backrezepten oft Bruchzahlen bei den Mengenangaben der Zutaten.

Abb. 1: Brüche multiplizieren im Alltag – Rezepte
Auf dem Bild siehst Du ein Rezept für die Zubereitung von 8 Muffins. Stell Dir vor, Du feierst Deinen Geburtstag und planst deshalb, für 8 Freunde Muffins zu backen. Bestimmt möchtest Du, dass jeder Gast mehr als einen Muffin essen darf. Keine Sorge, denn die Multiplikation von Brüchen hilft Dir, das Problem zu lösen, indem wir die Bruchzahlen im Rezept verdoppeln oder verdreifachen. Somit können Deine Freunde auch 2 oder 3 Muffins essen.

Wie Du das rechnest, erkläre ich Dir anschließend beim Bruchrechnen mit ganzen Zahlen. Vorher sollten wir aber lernen, wie ein Bruch aufgebaut ist, welche Arten es gibt und wie man sie mal rechnen muss.
Grundlagen für das Multiplizieren von Brüchen
Wenn Du Brüche multiplizieren möchtest, solltest Du wissen, wie schriftliches Addieren funktioniert. Ebenso ist bei einigen Rechnungen manchmal schriftliches Dividieren gefragt. Zudem sind das Einmaleins und das schriftliche Multiplizieren wichtige Voraussetzungen. Mehr zu den einzelnen Rechenarten lernst Du in der Hausaufgabenbetreuung.
Bevor wir nun beginnen, erläutere ich Dir noch schnell einige wichtige Grundlagen. Was ist ein Bruch? Er zeigt die Größe eines Anteils an einem Ganzen an. Das Ganze (ausgedrückt durch die Eins) kann man in kleinere Teile unterteilen.
Deine Pizza kannst Du zum Beispiel in 4 Teile teilen und eine ganze, eine halbe Pizza, eine viertel Pizza oder drei Viertel Pizza essen. Der Bruch zeigt an, dass von der ganzen Pizza nur ein Teil des Ganzen gemeint ist.
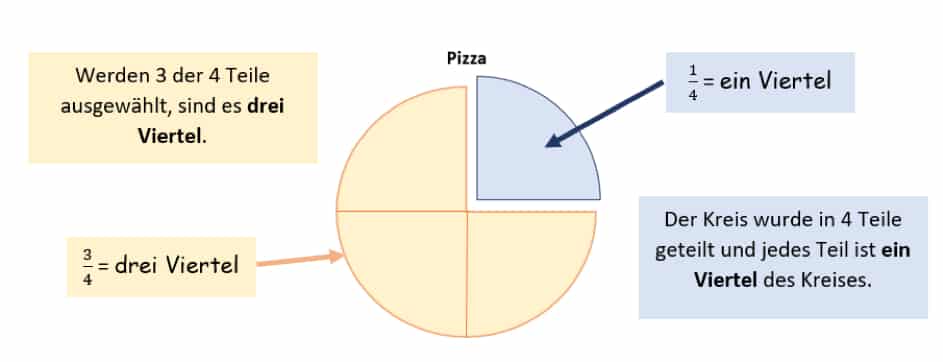
Abb. 2: Brüche multiplizieren – Anteile einer Pizza
Brüche sind durch einen waagerechten Bruchstrich getrennt und setzen sich aus einem Zähler (oberhalb des Bruchstrichs) und zudem einem Nenner (unterhalb) zusammen.

Abb. 3: Zähler und Nenner eines Bruchs
Die Arten
Beim Malnehmen von Brüchen rechnen wir mit unterschiedlichen Arten. Man unterscheidet dabei die folgenden Arten:
- echte (der Zähler ist kleiner als der Nenner):
- unechte (der Zähler ist größer als der Nenner oder gleich groß):
- gemischte (ganze Zahl + Bruch):
- Dezimalbrüche: 0,825
Um die Multiplikation leichter und schneller durchzuführen, musst Du kürzen oder eine Umwandlung in gemischte Brüche vornehmen. Besonders vor der Multiplikation ist ein geschicktes Kürzen ratsam.
Merke:
Einen Bruch kürzt Du, indem Du Zähler und Nenner durch die gleiche Zahl teilst.
Mit 2 kürzen:
Wie man einen gemischten Bruch in einen unechten umwandelt, erkläre ich Dir später nochmal ausführlich.
Multiplikation von echten Brüchen
Wir beginnen nun mit dem echten Bruch. Wie Du bereits weißt, ist der Zähler dabei kleiner als der Nenner: .
Als Rechenbeispiel für unsere erste Multiplikationsaufgabe nehmen wir daher die Aufgabe:
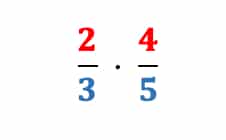
Hinweis:
Beim Multiplizieren mit Brüchen nimmst Du jeweils die beiden Zähler und die beiden Nenner mal: Zähler mal Zähler und Nenner mal Nenner.
Nimm jeweils die beiden Zähler 2 und 4 und die beiden Nenner 3 und 5 miteinander mal. Das kannst Du dabei leicht im Kopf rechnen. Falls Du damit noch Schwierigkeiten hast, solltest Du zuerst Kopfrechnen üben.
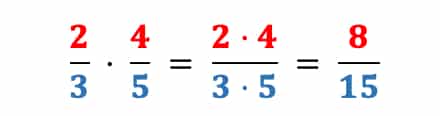
Schreibe Dein Ergebnis auf und prüfe, ob Du es kürzen kannst. Da der Zähler 8 und der Nenner 15 nicht durch die gleiche Zahl teilbar sind, kannst Du nicht mehr kürzen.
So funktioniert das Kürzen
Nicht immer kann man Zähler und Nenner so einfach im Kopf rechnen, versuchen wir es daher mit einem etwas schwierigeren Beispiel:
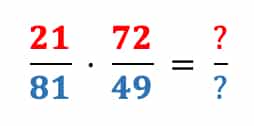
Hier sind Zähler und Nenner der Aufgabe so groß, dass wir die schriftliche Multiplikation zu Hilfe ziehen müssten, um zu rechnen. Vorher schauen wir uns die Zahlen aber genauer an und prüfen, ob sie einen gemeinsamen Teiler haben. Das heißt, wir sehen nach, ob man Zähler und Nenner durch die gleiche Zahl teilen kann. Falls es möglich ist, sollte man vorher immer kürzen.
Achtung:
Bei der Multiplikation darfst Du nicht nur Zähler und Nenner des gleichen Bruchs kürzen, sondern zudem auch über Kreuz: D.h. Du kannst den Zähler des einen Bruchs mit dem Nenner des Anderen kürzen.
Denn bei der Multiplikation spielt die Reihenfolge der Faktoren keine Rolle, d.h. ergibt dasselbe wie
. Das mathematische Gesetz, das die Vertauschung erlaubt, heißt auch Vertauschungsgesetz oder Kommutativgesetz (vgl. Krauthausen, 2006). Beim Kürzen solltest Du jedoch darauf achten, dass Zähler und Nenner so klein wie möglich sind, damit Du leicht multiplizieren kannst.
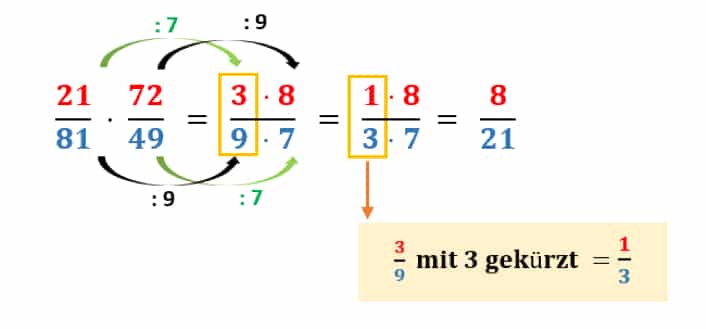
Abb. 4: Multiplizieren von Brüchen und Kürzen
Wenn Du Dir die Zahlen 21, 72, 81 und 49 genauer anschaust, merkst Du, dass 21 und 49 durch 7 teilbar sind und 81 und 72 durch 9. Zuerst kürzen wir die 21 und 49 mit 7. Rechne anschließend 21 : 7 und schreibe das Ergebnis 3 links oberhalb des Bruchstrichs. Danach rechnest Du 49 : 7 und schreibst das Ergebnis 7 rechts unterhalb. Nun bleiben noch 72 : 9 = 8 und 81 : 9 = 9. Schreibe diese Ergebnisse auch an die entsprechende Stelle. Anschließend darfst Du auch nochmal kürzen, indem Du Zähler und Nenner durch 3 teilst.
Drei Brüche multiplizieren
Nun weißt Du, wie man einen Bruch multipliziert und kannst sogar geschickt kürzen, um Deine Rechnung zu vereinfachen. Lass uns nun den nächsten Schritt wagen und 3 Brüche miteinander multiplizieren.
Tipp:
Wenn Du 3 Brüche miteinander malnehmen möchtest, musst Du alle drei Zähler und alle drei Nenner multiplizieren: Zähler • Zähler • Zähler und Nenner • Nenner • Nenner.
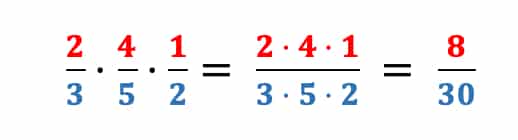
Durch das Vertauschungsgesetzt darfst Du auch hier wieder die Faktoren tauschen, um die Rechnung anschließend schneller im Kopf zu rechnen. Du kannst zum Beispiel anstatt auch
rechnen.
Aber Vorsicht, gerate nicht mit den Zählern und Nennern durcheinander. Diesen Fehler machen Schüler sehr häufig. Falls Du mehr über beliebte Fehler erfahren möchtest, sieh Dir die Veröffentlichung der Humboldt-Universität zu Berlin an.
Das Ergebnis kannst Du noch einmal mit 2 kürzen, indem Du Zähler und Nenner durch 2 teilst.
Dann erhältst Du .
Multiplizieren von unechten Brüchen
Du erinnerst Dich vielleicht, dass wir bei den verschiedenen Arten auch von unechten Brüchen gesprochen haben. Dabei ist der Zähler größer als der Nenner: .
Wenn wir die folgende Aufgabe mit zwei unechten Brüchen rechnen, erhalten wir auch beim Ergebnis einen Unechten. Diesen sollten wir in einen Gemischten umwandeln.
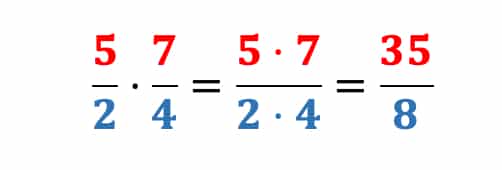
Achtung:
Um einen unechten Bruch in einen gemischten umzuwandeln, muss der Zähler durch den Nenner geteilt werden.
Um als gemischten Bruch zu schreiben, musst Du prüfen, wie oft der Nenner in den Zähler passt. Suche im Zähler 35 die nächstkleinere Zahl, die durch den Nenner 8 teilbar ist. 32 ist durch 8 teilbar.
Rechnung: 35 : 8 = 4 Rest 3.
Man kann sich auch vorstellen, dass man den Bruch aufteilt:
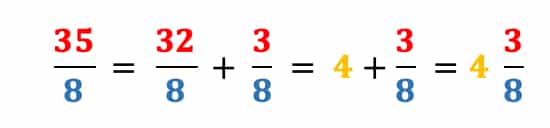
Brüche mal rechnen mit ganzen Zahlen
Du erinnerst Dich sicherlich noch, dass ich am Anfang erwähnt hatte, dass man Brüche oft in Rezepten findet und Mengenangaben manchmal verdoppeln oder verdreifachen muss. Als Beispiel nehmen wir nun aus unserem Muffin-Rezept das Mehl mit kg und verdreifachen die Menge, indem wir mal 3 rechnen:
.
Damit wir den Bruch mit einer ganzen Zahl multiplizieren können, nehmen wir eine Umwandlung der ganzen Zahl 3 vor und schreiben sie in einen unechten Bruch um. Man kann jede ganze Zahl (1,2, 3, 4, 5, 6, 7, 8, 9, …) auf diese Art umwandeln.
Tipp:
Du kannst ganze Zahlen in Brüche umwandeln, indem Du die ganze Zahl als Zähler setzt und die 1 als Nenner: .
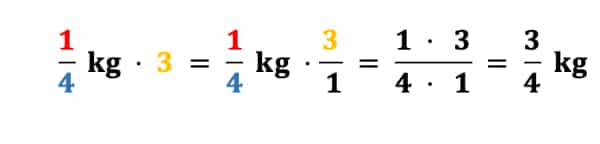
Das Schaubild verdeutlicht Dir nochmal, wie das mit ganzen Zahlen funktioniert:
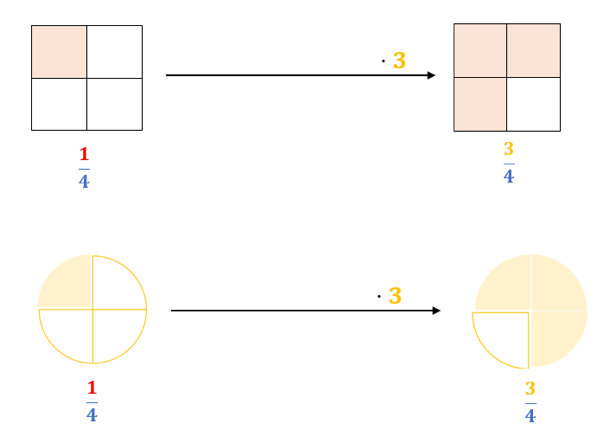
Abb. 5: Multiplikation von Brüchen mit ganzen Zahlen
Dezimalbrüche multiplizieren
Die Dezimalbruchrechnung ist besonders nützlich für Deinen Alltag und später auch im Beruf wichtig (vgl. Padberg, 2017). Du kannst auch Dezimalbrüche multiplizieren, allerdings benötigst Du hierfür meist die schriftliche Multiplikation.
Aufgabe: 2,17 • 8,76
Multipliziere so, als sei kein Komma vorhanden. Erst wenn Du das Ergebnis ermittelt hast, musst Du Dich um die Kommastellen kümmern. Mithilfe des Überschlags kannst Du feststellen, ob Du am Ende richtig gerechnet hast.
Überschlag: 2 • 9 = 18
Beim Rechnen beginnen wir mit der 8, der ersten Stelle des zweiten Dezimalbruchs. Danach rechnen wir mit der zweiten Stelle und abschließend mit der dritten Stelle weiter. Führe nun wie gewohnt die schriftliche Multiplikation durch und schau Dir das Ergebnis an.
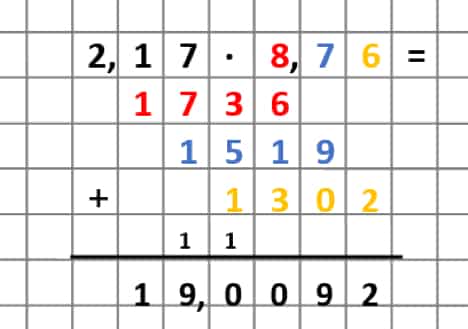
Abb. 6: Dezimalzahlen multiplizieren
Merke:
Das Ergebnis hat nach dem Komma so viele Stellen wie beide Dezimalbrüche zusammen.
Die Zahlen 2,17 und 8,76 haben je 2 Kommastellen, somit hat Dein Endergebnis 4 Kommastellen. Um das Komma zu setzen, musst Du von rechts nach links vier Stellen abzählen. Schau Dir nun den Überschlag an. Da 18 in der Nähe von 19,0092 liegt, hast Du richtig gerechnet.
Gemischte Brüche multiplizieren
Im oberen Abschnitt hast Du gelernt, wie man einen unechten Bruch in einen gemischten umwandelt. Jetzt möchte ich Dir für das Multiplizieren mit gemischten Brüchen die Umwandlung von einem gemischten Bruch in einen unechten erklären. Durch diesen Zwischenschritt fällt Dir das Rechnen deutlich leichter. Um beispielsweise mit einem anderen Bruch multiplizieren zu können, müssen wir die ganze Zahl 2 mit dem Nenner 3 malnehmen und den Zähler 1 addieren.
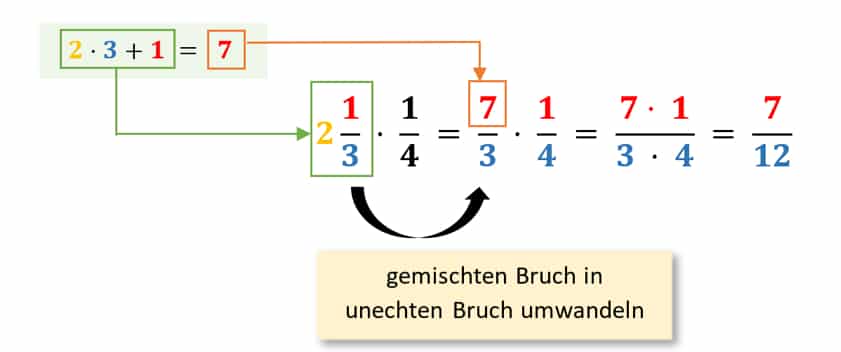
Abb. 7: Rechnen mit gemischten Brüchen
Merke:
Um einen gemischten Bruch zu multiplizieren, wandle ihn erst in einen unechten um. Rechne hierfür: Ganze Zahl • Nenner + Zähler. Das Ergebnis steht anschließend auf dem Bruchstrich; der Nenner bleibt beibehalten.
Übersicht – Multiplikation von Brüchen
Du hast nun gelernt, wie man Brüche multiplizieren kann. Hier findest Du zudem nochmal eine Übersicht der verschiedenen Rechenarten mit Beispielen und Erklärungen.
Tabelle 1: Eine Übersicht zur Zusammenfassung
| Multiplikation | Beispiel | Bemerkung |
| 2 Brüche multiplizieren | | Zähler mal Zähler und Nenner mal Nenner rechnen. |
| Mit ganzen Zahlen | | Zähler mal ganze Zahl rechnen und den Nenner beibehalten. |
| Dezimalbrüche | 1,25 • 0,7 = 0,875 | Schriftliche Multiplikation durchführen und anschließend die Kommastelle setzen. |
| Gemischte | | Bevor man einen gemischten Bruch multipliziert, sollte man ihn in einen unechten umwandeln. |
Übungsaufgaben zum Multiplizieren von Brüchen
Wie Du gesehen hast, ist das Brüche multiplizieren nicht schwer. Wenn Du Dich an die Regeln hältst, die Du oben gelernt hast, wirst Du in kürzester Zeit zum Profi. Hast Du noch Lust ein wenig zu üben? Dann sieh Dir unser Arbeitsblatt an. Denn wir haben Dir für jede Rechenart mehrere Aufgaben zusammengestellt. Einfache Erklärungen zu den Aufgaben findest Du zudem auf dem Lösungsblatt. Denn denke immer daran: Übung macht den Meister!
Du kannst stolz auf Dich sein, denn Du kennst nun alle Rechenregeln für die Multiplikation von Brüchen. Zur Erinnerung: Du musst Du Zähler mal Zähler und Nenner mal Nenner rechnen. Du weißt nun zudem, wie man echte, unechte, gemischte und auch Dezimalbrüche multipliziert. Mit diesen Kenntnissen kannst Du Multiplikationsaufgaben daher problemlos lösen. Falls Du das schon gut kannst, schau Dir auch an, wie man Brüche dividieren kann.
Literatur
Krauthausen, G., Scherer, P. (2006): Einführung in die Mathematikdidaktik. Heidelberg: Elsevier Spektrum Akademischer Verlag.
Padberg, F., Wartha, S. (2017): Didaktik der Bruchrechnung. Heidelberg: Elsevier Spektrum Akademischer Verlag.
FAQs – Bruch multiplizieren
Beim reinen Multiplizieren muss man nicht mit dem Kehrwert malnehmen. Dies ist erst bei der Division wichtig. Um den Kehrwert zu bilden, tauscht man einfach den Zähler und den Nenner eines Bruchs.
Man sollte vor dem Rechnen geschickt kürzen. Hier darf man zudem auch über Kreuz kürzen und den Zähler mit dem Nenner des anderen Bruchs kürzen.
Keine Sorge, Du musst keine neue Regel lernen, denn hierbei geht man wie gehabt vor. Hierfür multiplizierst Du daher wieder die beiden Zähler und die beiden Nenner miteinander.
Natürlich kannst Du auch vier Brüche miteinander malnehmen. Dafür musst Du lediglich jeweils die vier Zähler und die vier Nenner miteinander multiplizieren.
Du kannst zum Üben unser Arbeitsblatt nutzen. Ausführliche Erklärungen findest Du zudem auf dem Lösungsblatt. Hast Du noch offene Fragen? Unsere Trainer helfen Dir in unserer Mathe Nachhilfe gern.




