Schriftliches Subtrahieren

Schriftliches Subtrahieren wirst Du schnell und einfach lernen, wenn Du diesen Artikel liest! Ich zeige Dir ausführlich, wie die schriftliche Subtraktion funktioniert und demonstriere es zudem anhand von vielen Beispielen. Auch gehen wir gemeinsam schriftliches Subtrahieren mit Überschlag sowie die Subtraktion mehrerer Zahlen durch. Danach kannst Du Dein Wissen anhand unserer Aufgaben und Lösungen testen. Wirf anschließend einen Blick auf unsere Mathe Nachhilfe und vertiefe Dein Grundlagenwissen. Weitere Übungsaufgaben findest Du in unserer Hausaufgabenbetreuung. Nun lass uns loslegen!

Schriftliches Subtrahieren oder minus rechnen

Bevor ich Dir schriftliches Subtrahieren zeige, möchte ich mit Dir nochmal die Grundlagen der Subtraktion wiederholen. Stelle Dir vor, Du hast 9 Sammelkarten von denen Du 3 Deinem Freund schenken möchtest. Dann weißt Du sicherlich genau, dass Du danach noch 6 Karten übrighaben wirst. Dahinter steckt die Subtraktionsaufgabe:

Die Zahl, von welcher etwas abgezogen wird, heißt dabei Minuend. Der abgezogene Wert heißt Subtrahend und das Ergebnis wird Differenz genannt. Also ist bei der obigen Aufgabe die 9 der Minuend, die 3 der Subtrahend und das Ergebnis 6 die Differenz. Subtrahieren ist zudem genau das Gegenteil zum Addieren. Während Du beim Addieren auf dem Zahlenstrahl nach rechts wanderst, musst Du beim Subtrahieren entsprechend nach links wandern.

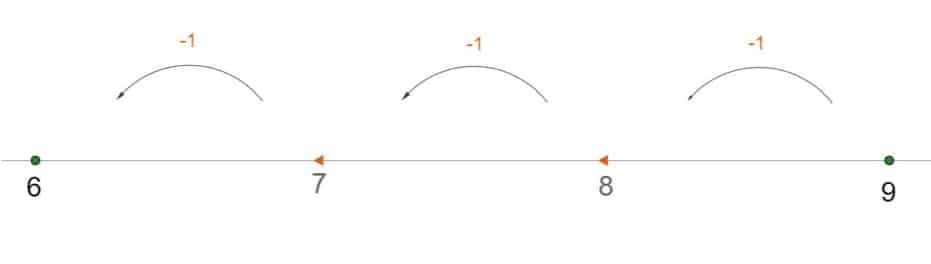
Genauer formuliert, beginnst Du beim Minuenden und läufst genauso viele Schritte nach links, wie Dein Subtrahend vorgibt. Im obigen Beispiel beginnen wir dabei bei der 9 und machen insgesamt 3 Schritte nach links. Damit landen wir schließlich bei der 6, was genau dem gesuchten Ergebnis entspricht. Du kannst Dir die Subtraktionsaufgabe aber auch so verdeutlichen: 9 – 6 = 3, da Du bei der 6 eine 3 ergänzen musst, um zur 9 zu gelangen. Du kannst also immer Subtrahieren, indem Du Dich fragst, wie viel Du dem Subtrahenden hinzufügen musst, um den Minuenden zu erhalten.

Die Universität Augsburg kommt zu dem Entschluss, dass dies vielen leichter fällt. Achte bei der Subtraktion immer darauf, dass der Minuend größer als der Subtrahend ist. Umgekehrt geht es zwar auch (Stichwort negative Zahlen), aber damit werden wir uns etwas später befassen.

Schriftlich subtrahieren mithilfe von Einern, Zehnern und Hundertern

Das schriftliche Subtrahieren werden wir vor allem für große Zahlen verwenden, indem wir sie auf die Subtraktion kleiner Zahlen zurückführen (vgl. Lauter (1979)). Hierfür verwenden wir die Zerlegung von Zahlen: In Einer, Zehner, Hunderter usw. Als Beispiel beginnen wir mit der Zahl 689:

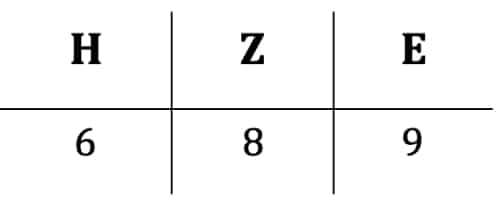
Wir möchten nun von dieser Zahl die Zahl 475 abziehen. Schreiben wir dabei beide in der obigen Zerlegung untereinander, so haben wir:

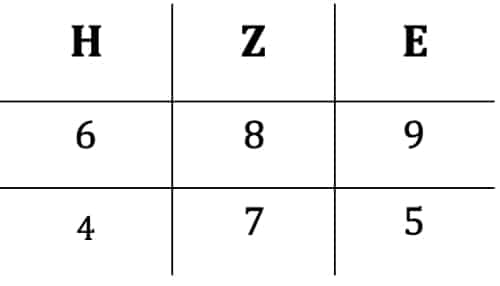
Für die schriftliche Subtraktion können wir nun die Einer, Zehner und Hunderter einzeln subtrahieren. Bei den Einern rechnen wir also 9 – 5 = 4. Für die Zehner haben wir 8 – 7 = 1 und bei den Hundertern dementsprechend 6 – 4 = 2. Die können wir ebenfalls tabellarisch schreiben:

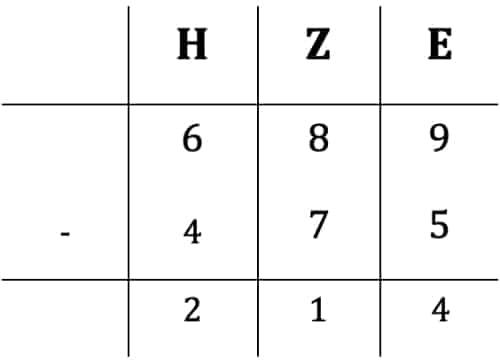
Dein Ergebnis lautet also 214. Damit hast Du Deine erste schriftliche Subtraktion bereits geschafft! Du brauchst also nur Spaltenweise zu subtrahieren und erhältst damit Dein Ergebnis. Du hast wahrscheinlich bereits bemerkt, dass in diesem Beispiel jede Ziffer des Minuenden größer war als die dazugehörige Ziffer des Subtrahenden. Falls dies nicht so ist, so subtrahieren wir mit Überschlag.

Mit Überschlag – Schriftliche Subtraktion

Beim schriftlichen Subtrahieren kommt es häufig vor, dass einzelne Ziffern Deines Minuenden kleiner sind als die des Subtrahenden. In diesem Fall benötigen wir einen Überschlag. Wie das geht, zeige ich Dir nun am Beispiel 91 – 26. Dazu schreiben wir die Subtraktion wieder tabellarisch untereinander:

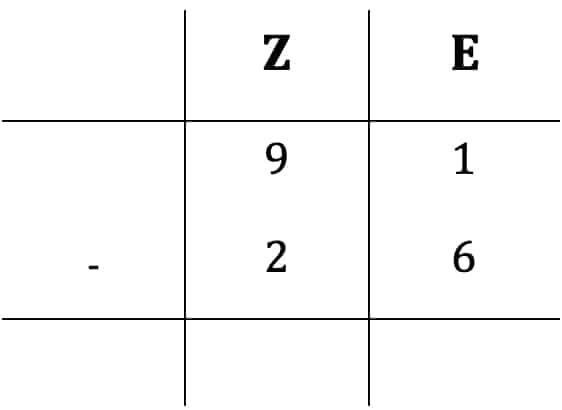
Bei den Einern ist die Ziffer 1 des Minuenden nun kleiner als die 6, welche beim Subtrahenden auftaucht. Dafür nehmen wir uns einen Zehner des Minuenden zur Hilfe, indem wir ihn als 10 Einer schreiben. Wir schreiben also:

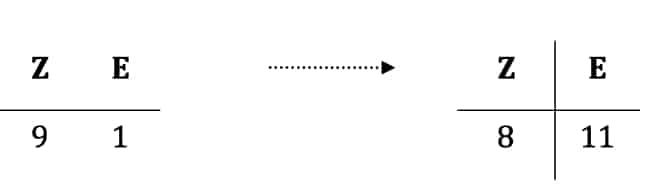
Bei der schriftlichen Subtraktion wird dies zu:

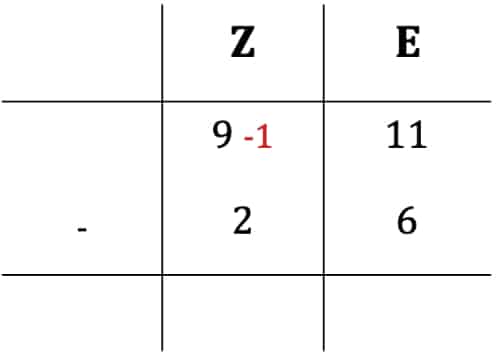
Da die 11 größer ist als die 6, kannst Du nun wie gewohnt schriftlich subtrahieren. Denke daran, dass Du von den 9 Zehnern eine zu den Einern verschoben hast. Das bedeutet, dass Du von den 9 Zehnern einen abziehen musst, es sind also noch 8 übrig! Da wir später schematisch schriftlich subtrahieren werden, ist es etwas einfacher, wenn wir stattdessen beim Subtrahenden eine 1 hinzufügen: 

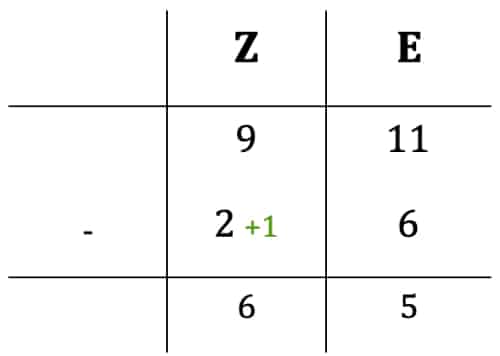
Auf diese Weise wird der Überschlag genauso notiert wie infolge schriftliches Addieren. Du siehst, dass Du nun wie gewohnt schriftlich subtrahieren kannst. Bei den Einern rechnest Du 11 – 6 = 5 und bei den Zehnern 9 – 3 = 6. Dein Ergebnis lautet also 65!

Schriftliches Subtrahieren als Schema

Nachdem Du die Grundlagen für die schriftliche Subtraktion verstanden hast, möchte ich Dir ein einfaches und schnelles Schema beibringen. Damit lernst Du zudem, wie Du viele und auch große Zahlen voneinander abziehen kannst. Dieses Schema bietet auch viele interessante digitale Anwendungen (vgl. Götze (2020)). Ich möchte Dir zunächst ein einfaches Beispiel zeigen.

Erklärung anhand eines Beispiels

In diesem Beispiel zeige ich Dir, wie Du schriftlich subtrahieren kannst:

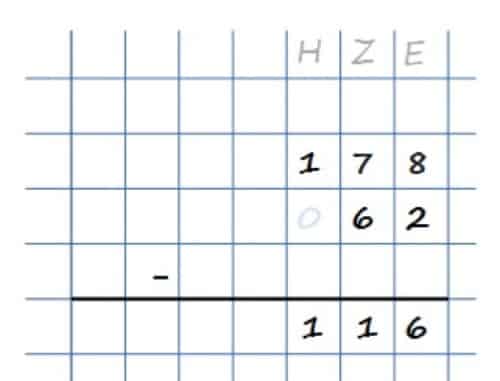
Dieses Beispiel behandelt die Subtraktion 178 – 62. Dazu beginnst Du rechts bei den Einern und berechnest 8 – 2 = 6. Das Ergebnis 6 kannst Du direkt unten notieren. Danach gehst Du zu den Zehnern und berechnest 7 – 6 = 1, welche Du wieder unten notieren kannst. Bei den Hundertern fällt Dir wahrscheinlich gleich auf, dass der Subtrahend keine, also 0 Hunderter hat. Ich habe dies in der obigen Rechnung kurz angedeutet. Hier kannst Du einfach die 1 vom Minuenden 178 direkt ins Ergebnis schreiben. Denn durch die Subtraktion  1 – 0 = 1 wird diese Ziffer nicht verändert. Als Ergebnis erhalten wir also 116!

Schriftlich subtrahieren – Beispiel mit Überschlag

Ich möchte Dir nun ein Beispiel zeigen, bei welchem Du einen Überschlag machen musst:

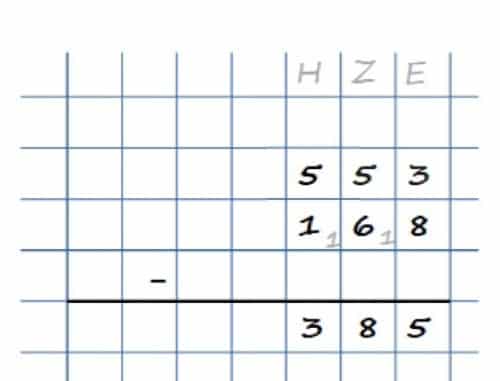
Wir beginnen wieder hinten und stellen fest, dass die 3 kleiner als die 8 ist. Also machen wir einen Überschlag und berechnen stattdessen 13 – 8 = 5. Dazu musst Du bei dem Zehner des Subtrahenden, also bei der 6 eine 1 als Überschlag notieren. Das Ergebnis der Einer ist 5, das kannst Du dann unten eintragen.

Bei den Zehnern müssen wir nun unten zu der 6 die 1 hinzufügen, also 5 – 7 rechnen. Da auch hier die 5 kleiner ist als die 7, nehmen wir die nächste Stelle zu Hilfe, berechnen also 15 – 7 = 8 und tragen bei den Hunderten wieder einen Überschlag von 1 ein. Das Ergebnis der Zehner ist 8 und wird wieder unten eingetragen. Bei den Hunderten musst Du nun wieder den Überschlag berücksichtigen, indem Du 1 + 1= 2 rechnest und dann 5 – 2 = 3. Also trägst Du unten 3 in das Ergebnis ein und wir erhalten insgesamt 385!

Mit mehreren Zahlen

Ich möchte Dir nun zeigen, wie Du mithilfe dieses Schemas einfach viele Zahlen schriftlich subtrahieren kannst. Dazu eine kleine Bemerkung: Wenn Du z. B. 15 – 3 – 2 berechnen möchtest, gibt es einen kleinen Trick. Die Subtrahenden 3 und 2 kannst Du einfach addieren, also 2 + 3 = 5 und dann stattdessen 15 – 5 rechnen!

Im Schema kannst Du das besonders einfach umsetzen. Sehen wir uns zum Beispiel die Rechenaufgabe 8628 – 252 – 184 im Schema an: 

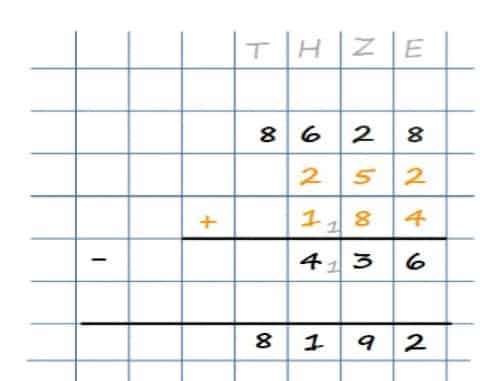
Vor der schriftlichen Subtraktion addieren wir zunächst die Subtrahenden schriftlich. Bei der Addition erhältst Du als Ergebnis 436. Also müssen wir anschließend 8628 – 436 schriftlich subtrahieren. Hierzu gehst Du wie gewohnt vor: Zuerst berechnest Du 8 – 6 = 2 und trägst die 2 unten im Ergebnis ein. 

Danach musst Du 2 – 3 berechnen. Wahrscheinlich hast Du schon bemerkt, dass Du hier einen Überschlag brauchst! Also rechnest Du 12 – 3 = 9, trägst diese Zahl unten im Ergebnis ein und notierst den Überschlag 1 bei den Hundertern. Um weiter zu rechnen, müssen wir zuerst 4 + 1 = 5 beachten und können dann 6 – 5 = 1 berechnen. Also kommt bei den Hundertern unten eine 1 in das Ergebnis. Da der Subtrahend keine Tausender hat, erhältst Du als letzte Stelle eine 8. Damit hast Du erfolgreich 8628 – 252 – 184 = 8192 berechnet!

Schriftlich subtrahieren mit Komma

Es kann vorkommen, dass Du keine ganze Zahl subtrahieren möchtest, sondern eine sogenannte Dezimalzahl. Das ist eine Zahl, die ein Komma aufweist. Die Zahlen kennst Du ja bereits vom Zahlenstrahl. Aber was kannst Du machen, wenn Du die Stelle zwischen zwei Zahlen auf dem Zahlenstrahl benennen möchtest? Dazu kannst Du Dezimalzahlen verwenden, die auch Kommazahlen genannt werden. Sie teilen sich in einen Bereich vor dem Komma und einen hinter dem Komma auf.

Eine Subtraktionsaufgabe mit Kommazahlen löst Du genau wie eine mit ganzen Zahlen. Du musst die Kommazahlen nur untereinanderschreiben und kannst dann so vorgehen, wie wir es oben geübt haben. Pass aber auf, dass Du die Stellen der Kommazahlen richtig einträgst und beim Ergebnis das Komma an die richtige Stelle setzt.

Übersicht – schriftliche Subtraktion

Du hast nun schon die Regeln der schriftlichen Subtraktion kennengelernt. Hier findest Du zur Erinnerung eine Übersicht der Grundregeln mit Rechenbeispielen und einer kurzen Erklärung. Vielleicht kannst Du anschließend noch Kopfrechnen üben?

Tabelle 1: Schriftliche Subtraktion Übersicht

Subtraktion	Beispiele	Bemerkungen
Ohne Überschlag	96 – 21	Subtraktion der einzelnen Ziffern führt zum Ergebnis.
Mit Überschlag	121 – 65	Statt 1 – 5 wird 11 – 5 bei den Einern berechnet. Der übertragene Zehner wird als Überschlag berücksichtigt.
Mehrerer Zahlen	954 – 356 – 248 – 45	Zuerst Addition aller Subtrahenden und anschließende Subtraktion von Minuend und dieser Summe.

Schriftliches Subtrahieren Aufgaben

Damit Du anschließend gleich weiter üben kannst, haben wir für Dich das  Arbeitsblatt schriftliche Subtraktion erstellt. Also setz Dich doch gleich an die Aufgaben und stelle unter Beweis, wie viel Du gelernt hast! Deine Ergebnisse kannst Du am Ende mit den Lösungen der Subtraktionsaufgaben überprüfen. Wir wünschen Dir viel Spaß!

Die schriftliche Subtraktion ist einfach! Falls alle Ziffern des Subtrahenden kleiner als die des Minuenden sind, kannst Du einfach spaltenweise subtrahieren. Ist das nicht so, dann hilft Dir Subtrahieren mit Überschlag weiter – ganz ähnlich wie bei der Addition. Die schriftliche Subtraktion mehrerer Zahlen ist kein Problem, sobald Du zuerst alle Subtrahenden addierst. Alles in einem ist schriftliches Subtrahieren schnell zu lernen, einfach zu verstehen und gehört zudem wie die anderen drei schriftlichen Rechnerverfahren zu den Grundlagen.

Literatur

Lauter, Josef (1979): Methodik der Grundschulmathematik. Auer-Verlag, Köln.

Götze, Daniela (2020): Elemente der Arithmetik verstehen lernen – professionsorientiert, vorstellungsbasiert und digital. Springer Spektrum, Wiesbaden.

FAQs – Schriftlich subtrahieren